Question

【题目】四边形ABCD是正方形，E、F分别是DC和CB的延长线上的点，且DE=BF，连接AE、AF、EF．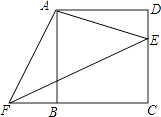

（1）求证：△ADE≌△ABF；
（2）若BC=12，DE=5，求△AEF的面积．

Answer 1

【答案】
（1）

解：∵四边形ABCD是正方形，

∴AD=AB，∠D=∠ABC=90°，

而F是CB的延长线上的点，

∴∠ABF=90°，

在△ADE和△ABF中，

∵ ，

∴△ADE≌△ABF（SAS）

（2）

解：∵BC=12，∴AD=12，

在Rt△ADE中，DE=5，AD=12，

∴AE= =13，

∵△ABF可以由△ADE绕旋转中心 A点，按顺时针方向旋转90°得到，

∴AE=AF，∠EAF=90°，

∴△AEF的面积= AE2= ×169=84.5

【解析】（1）由正方形的性质得出AD=AB，∠D=∠ABC=∠ABF=90°，依据“SAS”即可证得；（2）根据勾股定理求得AE=13，再由旋转的性质得出AE=AF，∠EAF=90°，从而由面积公式得出答案．