题目内容
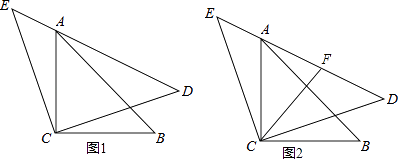
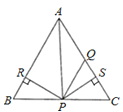
【题目】如图所示,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则下列三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS中( )
A. 全部正确 B. 仅①和②正确 C. 仅①正确 D. 仅①和③正确
【答案】B
【解析】∵PR=PS,PR⊥AB于R,PS⊥AC于S,
∴∠PAB=∠PAC,∠PSA=∠PRA=90°,
在△PAR和△PAS中,
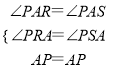 ,
,
∴△PAR≌△PAS(AAS),
∴AR=AS,∴①正确;
∵AQ=PQ,
∠CAP=∠APQ,
∵∠CAP=∠BAP,
∴∠BAP=∠APQ,
∴PQ∥AB,∴②正确;
∵PR⊥AB,PS⊥AC,
∴∠PRB=∠PSC=90°,
∴PQ>PS,
∵PR=PS,
∴PQ>PR,
∴不能推出△BRP≌△CQP,∴③错误.
故选B.

练习册系列答案
相关题目
【题目】某商场进行有奖促销活动.活动规则:购买500元商品就可以获得一次转转盘的机会(转盘被分为5个扇形区域,分别是特等奖、一等奖、二等奖、三等奖、纪念奖),转动转盘停止后,指针指在哪个获奖区域就可以获得该区域相应等级奖品一件(奖品设置如图所示).商场工作人员在制作转盘时,将获奖区域扇形圆心角分配如下表:
奖次 | 特等奖 | 一等奖 | 二等奖 | 三等奖 | 纪念奖 |
圆心角 | 1° | 10° | 30° | 90° | 229° |
(1)转动一次转盘,获得圆珠笔的概率是多少?
(2)如果不用转盘,请设计一种等效活动方案
(要求写清替代工具和活动规则).