题目内容
【题目】在平面直角坐标系中,点![]() ,
,![]() 为反比例函数
为反比例函数![]() 上的两个动点,以
上的两个动点,以![]() ,
,![]() 为顶点构造菱形
为顶点构造菱形![]() .
.
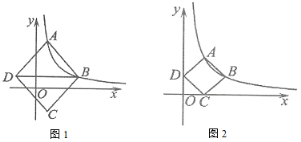
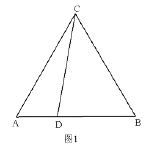
(1)如图1,点![]() ,
,![]() 横坐标分别为1,4,对角线
横坐标分别为1,4,对角线![]() 轴,菱形
轴,菱形![]() 面积为
面积为![]() .求
.求![]() 的值.
的值.
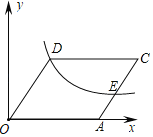
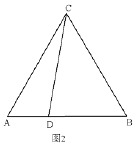
(2)如图2,当点![]() ,
,![]() 运动至某一时刻,点
运动至某一时刻,点![]() ,点
,点![]() 恰好落在
恰好落在![]() 轴和
轴和![]() 轴正半轴上,此时
轴正半轴上,此时![]() .求点
.求点![]() ,
,![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)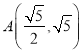 ,
,
【解析】
(1) 由菱形的性质可得BD=2BE=6, AC⊥DB,由菱形的面积公式可求AC=![]() ,设点B (4,a),则点A (1,
,设点B (4,a),则点A (1, ![]() +a),代入解析式可求a的值,即可求k的值;
+a),代入解析式可求a的值,即可求k的值;
(2)过点A作AE⊥y轴于点E,过点B作BF⊥x轴于点F,设点A (m, ![]() ),由全等三角形的性质可得AE=DO=CF=m, DE=OC=BF=
),由全等三角形的性质可得AE=DO=CF=m, DE=OC=BF=![]() -m,可求点B坐标,代入解析式可求解.
-m,可求点B坐标,代入解析式可求解.
(1)如图,连结![]() 交
交![]() 于点
于点![]() .
.
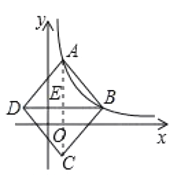
∵![]() ,
,![]() 的横坐标分别为1,4,
的横坐标分别为1,4,![]() 轴.
轴.
∴![]()
∵菱形![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]()
∴![]() ,AC⊥DB
,AC⊥DB
∵![]()
∴![]()
∴AE=CE=![]()
设![]() ,
,![]()
∵点![]() ,
,![]() 都在反比例函数
都在反比例函数![]() 上
上
∴![]() 解得
解得![]() .
.
∴![]() .
.
(2)如图,过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴.
轴.
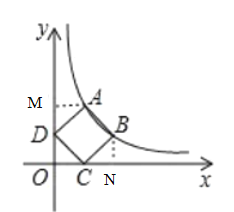
由(1)可知点![]() ,
,![]() 在反比例函数
在反比例函数![]() 上,设
上,设![]()
∵菱形![]() 中,
中,![]()
∴四边形![]() 是正方形
是正方形
∴![]() ,
,![]()
∴∠ADM+∠MAD=90°,∠MDA+∠CDO=90°,∠DCO+∠CDO=90°,∠BCN+∠DCO=90°,
∴∠MAD=∠CDO=∠BCN,且∠AMD=∠DOC=∠CNB90°,AD=CD=BC,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
∴![]() .
.
由此可知点![]() 的坐标为
的坐标为![]() ,
,
将点![]() 代入
代入![]() 得
得![]()
![]() 或
或![]() (舍去)
(舍去)
∴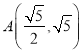 ,
,

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目