题目内容
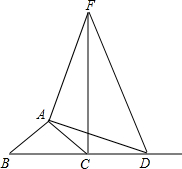等腰直角三角形ABC和等腰直角三角形ADF放在一起，使B、C、D三点在同一直线上，
求证：FC⊥BD．
证明；∵三角形ABC和三角形ADF都是等腰直角三角形，
∴AB=AC，∠B=∠ACB=45°，AF=AD，
∴△ABD≌△CAF，
∴∠FCA=∠B=45°，
∵B、C、D三点在同一直线上，
∴∠FCB=∠ACB+∠FCA=45°+45°=90°，
∴FC⊥BD．
分析：要证FC⊥BD，需证∠FCB=90°，需证∠ACB+∠FCA=90°可由等腰直角三角形提供．求证△ABD≌△CAF即可．
点评：本题考查了全等三角形的判定和性质；全等问题要注意找条件，有些条件需在图形是仔细观察，认真推敲方可．做题时，一定要仔细认真．
∴AB=AC，∠B=∠ACB=45°，AF=AD，
∴△ABD≌△CAF，
∴∠FCA=∠B=45°，
∵B、C、D三点在同一直线上，
∴∠FCB=∠ACB+∠FCA=45°+45°=90°，
∴FC⊥BD．
分析：要证FC⊥BD，需证∠FCB=90°，需证∠ACB+∠FCA=90°可由等腰直角三角形提供．求证△ABD≌△CAF即可．
点评：本题考查了全等三角形的判定和性质；全等问题要注意找条件，有些条件需在图形是仔细观察，认真推敲方可．做题时，一定要仔细认真．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
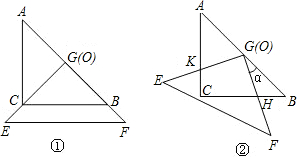把两个全等的等腰直角三角形ABC和EFG（其直角边长均为4）叠放在一起（如图①），且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合．现将三角板EFG绕O点逆时针旋转（旋转角α满足条件：0°＜α＜90°），四边形CHGK是旋转过程中两三角板的重叠部分（如图②）．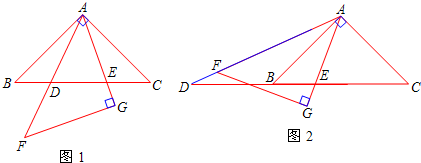
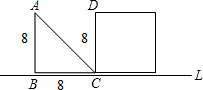AB与CD重合．设x秒时，三角形与正方形不重叠部分的面积为ym2．
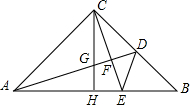如图，等腰直角三角形△ABC中，∠ACB=90°，点D是BC的中点，CE⊥AD于点F交AB于点E，CH是AB上的高交AD于点G．