题目内容
 如图,等腰直角三角形△ABC中,∠ACB=90°,点D是BC的中点,CE⊥AD于点F交AB于点E,CH是AB上的高交AD于点G.
如图,等腰直角三角形△ABC中,∠ACB=90°,点D是BC的中点,CE⊥AD于点F交AB于点E,CH是AB上的高交AD于点G.(1)找出图中的全等三角形;
(2)找出与∠ADC相等的角,并请说明理由.
分析:(1)根据等腰直角三角形的性质以及利用点D是BC的中点和CE⊥AD以及CH是AB上的高分别得出全等三角形即可;
(2)首先根据全等三角形的判定得出△ACG≌△BCE以及△DCG≌△DBE,即可得出∠CDG=∠BDE.
(2)首先根据全等三角形的判定得出△ACG≌△BCE以及△DCG≌△DBE,即可得出∠CDG=∠BDE.
解答:解:(1)①△ACH≌△BCH;②△ACG≌△CBE;
③△AHG≌△CHE;④△CDG≌△BDE;
(2)∠ADC=∠ACF=∠BDE,
理由:∵∠ACD=90°,∠AFC=90°,
∴∠ADC=∠ACF,
∵等腰直角三角形△ABC中,∠ACB=90°,CH是AB上的高,
∴AC=BC,CH=AH=BH,∠CAH=∠ACH=∠BCH=∠B=45°,
∵CE⊥AD,∴∠BCE+∠ACF=∠CAD+∠ACF=90°,
∴∠BCE=∠CAD
在△ACG和△BCE中,
∴△ACG≌△BCE(ASA),
∴CG=BE,
∵点D是BC的中点,∴CD=BD.
在△DCG和△DBE中,
∴△DCG≌△DBE(SAS),
∴∠CDG=∠BDE.
③△AHG≌△CHE;④△CDG≌△BDE;
(2)∠ADC=∠ACF=∠BDE,
理由:∵∠ACD=90°,∠AFC=90°,

∴∠ADC=∠ACF,
∵等腰直角三角形△ABC中,∠ACB=90°,CH是AB上的高,
∴AC=BC,CH=AH=BH,∠CAH=∠ACH=∠BCH=∠B=45°,
∵CE⊥AD,∴∠BCE+∠ACF=∠CAD+∠ACF=90°,
∴∠BCE=∠CAD
在△ACG和△BCE中,
|
∴△ACG≌△BCE(ASA),
∴CG=BE,
∵点D是BC的中点,∴CD=BD.
在△DCG和△DBE中,
|
∴△DCG≌△DBE(SAS),
∴∠CDG=∠BDE.
点评:此题主要考查了等腰直角三角形的性质以及全等三角形的判定与性质,根据已知得出△ACG≌△BCE是解题关键.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 如图,等腰直角三角形ABC绕C点按顺时针旋转到△A1B1C1的位置(A、C、B1在同一直线上),∠B=90°,如果AB=1,那么AC运动到A1C1所经过的图形的面积是
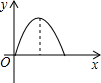
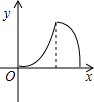
如图,等腰直角三角形ABC绕C点按顺时针旋转到△A1B1C1的位置(A、C、B1在同一直线上),∠B=90°,如果AB=1,那么AC运动到A1C1所经过的图形的面积是 如图,等腰直角三角形ABC的腰长与正方形DEFG的边长相符,且边AC与DE在同一直线l上,△ABC从如图所示的起始位置(A、E重合),沿直线l水平向右平移,直至C、D重合为止.设△ABC与正方形DEFG重叠部分的面积为y,平移的距离为x,则y与x之间的函数关系大致是( )
如图,等腰直角三角形ABC的腰长与正方形DEFG的边长相符,且边AC与DE在同一直线l上,△ABC从如图所示的起始位置(A、E重合),沿直线l水平向右平移,直至C、D重合为止.设△ABC与正方形DEFG重叠部分的面积为y,平移的距离为x,则y与x之间的函数关系大致是( )

 如图,等腰直角三角形ABC中,∠BAC=90°,D、E分别为AB、AC边上的点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M.
如图,等腰直角三角形ABC中,∠BAC=90°,D、E分别为AB、AC边上的点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M. 如图,等腰直角三角形AEF的顶点E在等腰直角三角形ABC的边BC上.AB的延长线交EF于D点,其中∠AEF=∠ABC=90°.
如图,等腰直角三角形AEF的顶点E在等腰直角三角形ABC的边BC上.AB的延长线交EF于D点,其中∠AEF=∠ABC=90°.