题目内容
如图(单位:m),等腰直角三角形ABC以2米/秒的速度沿直线L向正方形移动,直到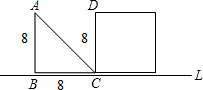 AB与CD重合.设x秒时,三角形与正方形不重叠部分的面积为ym2.
AB与CD重合.设x秒时,三角形与正方形不重叠部分的面积为ym2.(1)写出y与x的关系式,并写出自变量x的取值范围;
(2)请画出此函数的图象;
(3)当不重叠部分的面积是三角形面积的一半时,三角形移动了多长时间?
分析:(1)根据题意可知,三角形与正方形重合部分是个等腰直角三角形,且直角边都是2x,据此可得出三角形与正方形不重叠部分的面积y、x的函数关系式;
(2)根据(1)中的函数关系式画出图象即可;
(3)将正方形的面积的一半代入(1)的函数关系式中,即可求得x的值.(其实此时AB与DC重合,也就是说等腰三角形运动的距离正好是正方形的边长8m.)
(2)根据(1)中的函数关系式画出图象即可;
(3)将正方形的面积的一半代入(1)的函数关系式中,即可求得x的值.(其实此时AB与DC重合,也就是说等腰三角形运动的距离正好是正方形的边长8m.)
解答:解:(1)因为三角形与正方形重合部分是个等腰直角三角形,且直角边都是2x,
∴重叠部分的面积=2x2,
又因为△ABC的面积为:
×8×8=32m2,
所以y=32-2x2,(0≤x≤4).
(2)所画图象如下所示:
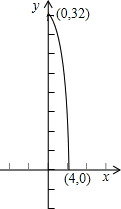
(3)在y=32-2x2中
当y=16时,2x2=16,
所以x2=8,解得x=2
秒(负值舍去).
当不重叠部分的面积是三角形面积的一半时,三角形移动了2
秒.
∴重叠部分的面积=2x2,
又因为△ABC的面积为:
| 1 |
| 2 |
所以y=32-2x2,(0≤x≤4).
(2)所画图象如下所示:

(3)在y=32-2x2中
当y=16时,2x2=16,
所以x2=8,解得x=2
| 2 |
当不重叠部分的面积是三角形面积的一半时,三角形移动了2
| 2 |
点评:本题考查了二次函数的实际应用,难度适中,命题立意:考查综合应用知识,分析问题的能力.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
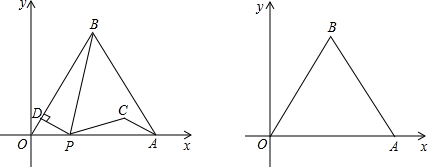
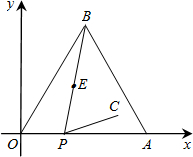 点为点E,将线段PE绕点P按顺时针方向旋转60°得PC.
点为点E,将线段PE绕点P按顺时针方向旋转60°得PC. 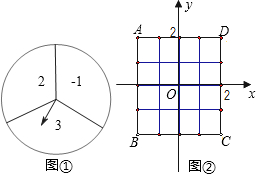 的数字为纵坐标).
的数字为纵坐标).