Question

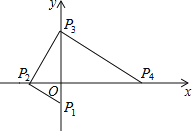
【题目】如图，点P1，P2，P3，P4均在坐标轴上，且P1P2⊥P2P3，P2P3⊥P3P4，若点P1，P2的坐标分别为（0，﹣1），（﹣2，0），求点P4的坐标．

Answer 1

【答案】（8，0）．

【解析】根据相似三角形的性质求出P3D的坐标，再根据相似三角形的性质计算求出OP4的长，得到答案．

解：∵点P1，P2的坐标分别为（0，﹣1），（﹣2，0），

∴OP1=1，OP2=2，

∵Rt△P1OP2∽Rt△P2OP3，

∴=，即=，

解得，OP3=4，

∵Rt△P2OP3∽Rt△P3OP4，

∴=，即=，

解得，OP4=8，

则点P4的坐标为（8，0），

故答案为：（8，0）．

“点睛”本题考查的是相似三角形的判定和性质以及坐标与图形的性质，掌握相似三角形的判定定理和性质定理是解题的关键．