题目内容
【题目】如图,Rt△ABC中,∠BCA=90°,AC=BC,点D是BC的中点,点F在线段AD上,DF=CD,BF交CA于E点,过点A作DA的垂线交CF的延长线于点G,下列结论:①CF2=EFBF;②AG=2DC;③AE=EF;④AFEC=EFEB.其中正确的结论有________
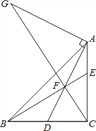
【答案】①②④.
【解析】根据等边对等角的性质求出∠DCF=∠DFC,然后求出DF=DB,根据等边对等角求出∠DBF=∠DFB,然后求出∠BFC是直角,根据直角三角形的性质求出△BCF和△CEF相似,根据相似三角形对应边成比例列式整理即可得到①正确;根据互余关系求出∠G=∠ACG,再根据等角对等边的性质求出AG=AC,然后求出AG=BC,然后利用“角角边”证明△BCE和△AGF全等,根据全等三角形对应边相等可得AG=BC,从而判断②正确;根据角的互余关系可以求出∠EAF+∠ADC=90°,∠AFE+∠DFC=90°再根据∠ADC的正切值为2可知∠ADC≠60°,然后求出∠FDC≠∠DFC,然后求出∠EAF≠∠EFA,从而得到AE≠EF,判断出③错误;根据根据直角三角形的性质求出△CEF和△BCE相似,根据相似三角形的对应边成比例列式求出EC2=EFEB,再根据全等三角形对应边相等可得AF=CE,从而判断出④正确.
解:∵DF=CD,
∴∠DCF=∠DFC,
∵AC=BC,点D是BC的中点,
∴DF=DB=DC,
∴∠DBF=∠DFB,
又∵∠DBF+∠DFB+∠DFC+∠DCF=180°,
∴∠BFC=![]() ×180°=90°,
×180°=90°,
∴CF⊥BE,
∴Rt△BCF∽Rt△CEF,
∴![]() =
=![]() ,
,
∴CF2=EFBF,故①正确;
∵AG⊥AD,
∴∠G+∠AFG=90°,
又∵∠ACG+∠DCF=90°,∠DCF=∠DFC=∠AFG,
∴∠G=∠ACG,
∴AG=AC,
∵AC=BC,
∴AG=BC,
又∵∠CBE=∠ACG,
∴∠CBE=∠G,
在△BCE和△AGF中,
∵∠GAF=∠BCE=90°,∠CBE=∠G,AG=BC,,
∴△BCE≌△AGF(AAS),
∴AG=BC,
∵点D是BC的中点,
∴BC=2DC,
∴AG=2DC,故②正确;
根据角的互余关系,∠EAF+∠ADC=90°,∠AFE+∠DFC=90°,
∵tan∠ADC=2,
∴∠ADC≠60°,
∵∠DCF=∠DFC,
∴∠FDC≠∠DFC,
∴∠EAF≠∠EFA,
∴AE≠EF,故③错误;
∵∠ACB=90°,CF⊥BE,
∴△CEF∽△BCE,
∴![]() =
=![]() ,
,
∴EC2=EFEB,
∵△BCE≌△AGF(已证),
∴AF=EC,
∴AFEC=EFEB,故④正确;
所以,正确的结论有①②④.
“点睛”本题考查了相似三角形的判定与性质,全等三角形的判定与性质,等腰直角三角形的性质,根据等角对等边以及等边对等角的性质求出AG=AC,然后证明△BCE和△AGF全等是证明的关键,也是本题的难点.