题目内容
【题目】抛物线![]() 经过点A(-4,0),B(2,0)且与
经过点A(-4,0),B(2,0)且与![]() 轴交于点C.
轴交于点C.
(1)求抛物线的解析式;
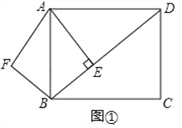
(2)如图1,P为线段AC上一点,过点P作![]() 轴平行线,交抛物线于点D,当△ADC的面积最大时,求点P的坐标;
轴平行线,交抛物线于点D,当△ADC的面积最大时,求点P的坐标;
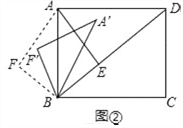
(3)如图2,抛物线顶点为E,EF⊥x轴子F点,M、N分别是![]() 轴和线段EF上的动点,设M的坐标为(m,0),若∠MNC=90°,请指出实数m的变化范围,并说明理由.
轴和线段EF上的动点,设M的坐标为(m,0),若∠MNC=90°,请指出实数m的变化范围,并说明理由.
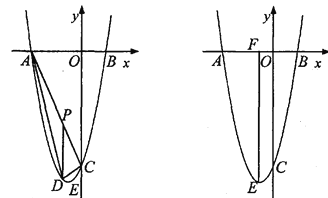
图1 图2
【答案】(1)y=x2+2x﹣8;(2)(﹣2,﹣4);(3)﹣10≤m≤15
【解析】试题分析:(1)只需用待定系数法就可求出抛物线的解析式;
(2)可用待定系数法求出直线AC的解析式为y=-2x-8,设点P的坐标为(a,-2a-8),则点D(a,a2+2a-8),(-4<a<0),然后用割补法求得S△ADC=-2(a+2)2+8,从而可求出△ADC的面积最大时点P的坐标;
(3)易求得OF=1、EF=9、OC=8.设FN=n,(0≤n≤9),然后分三种情况(Ⅰ.M与点F重合,Ⅱ.M在点F左侧,Ⅲ.M在点F右侧)讨论,运用相似三角形的性质均可得到m=-n2+8n-1(0≤n≤9).由m=-n2+8n-1=-(n-4)2+15可得到m最大值为15,再由n=0时m=-1,n=9时m=-10可得m最小值为-10,从而可得到m的取值范围.
解:(1)∵抛物线y=x2+bx+c经过点A(﹣4,0),B(2,0),
∴![]() ,
,
解得![]() .
.
∴抛物线的解析式为y=x2+2x﹣8.
(2)如图1,
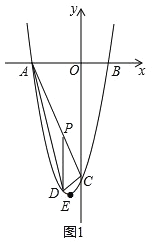
令x=0,得y=﹣8,
∴点C的坐标为(0,﹣8).
设直线AC的解析式为y=kx+t,
则![]() ,
,
解得:![]() ,
,
∴直线AC的解析式为y=﹣2x﹣8.
设点P的坐标为(a,﹣2a﹣8),则点D(a,a2+2a﹣8),(﹣4<a<0),
∴PD=(﹣2a﹣8)﹣(a2+2a﹣8)=﹣a2﹣4a,
∴S△ADC=S△APD+S△CPD
=![]() PD[a﹣(﹣4)]+
PD[a﹣(﹣4)]+![]() PD(0﹣a)
PD(0﹣a)
=2PD=﹣2(a2+4a)
=﹣2(a+2)2+8,
∴当a=﹣2时,S△ADC取到最大值为8,此时点P的坐标为(﹣2,﹣4).
(3)由y=x2+2x﹣8=(x+1)2﹣9得E(﹣1,﹣9)、C(0,﹣8),
则有OF=1、EF=9、OC=8.
设FN=n,(0≤n≤9),
Ⅰ.当M与点F重合时,此时m=﹣1,n=8,显然成立;
Ⅱ.当M在点F左侧,作NQ⊥y轴于点Q,如图2①,此时m<﹣1.

∵∠MNC=∠FNQ=90°,∴∠MNF=∠CNQ.
∵∠MFN=∠CQN=90°,
∴△MFN∽△CQN,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴m=﹣n2+8n﹣1.
Ⅲ.当M在点F右侧,作NQ′⊥y轴于点Q′,如图2②,此时m>﹣1.

∵∠MNC=∠FNQ′=90°,∴∠MNF=∠CNQ′.
∵∠MFN=∠CQ′N=90°,
∴△MFN∽△CQ′N,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴m=﹣n2+8n﹣1.
综上所述:m=﹣n2+8n﹣1,(0≤n≤9).
∴m=﹣n2+8n﹣1=﹣(n﹣4)2+15,
∴当n=4时,m取到最大值为15.
∵n=0时m=﹣1,n=9时m=﹣10,
∴m取到最小值为﹣10,
∴m的取值范围是﹣10≤m≤15.

 阅读快车系列答案
阅读快车系列答案【题目】NBA季后赛正如火如荼地进行着,詹姆斯率领的骑士队在第三场季后赛中先落后25分的情况
下实现了大逆转.该场比赛中詹姆斯的技术统计数据如下表所示:
技术 | 上场时间 (分钟) | 出手投篮(次) | 投中 (次) | 罚球 得分 | 篮板 (个) | 助攻 (次) | 个人 总得分 |
数据 | 45 | 27 | 14 | 7 | 13 | 12 | 41 |
【注:表中出手投篮次数和投中次数均不包括罚球,个人总得分来自2分球和3分球的得分以及罚
球得分.】根据以上信息,求出本场比赛中詹姆斯投中2分球和3分球的个数.