题目内容
(2013•葫芦岛一模)(1)如图1,在矩形ABCD中,AB=2BC,M是AB的中点.直接写出∠BMD与∠ADM的倍数关系;
(2)如图2,若四边形ABCD是平行四边形,AB=2BC,M是AB的中点,过C作CE⊥AD与AD所在直线交于点E.
①若∠A为锐角,则∠BME与∠AEM有怎样的倍数关系,并证明你的结论;
②当0°<∠A<
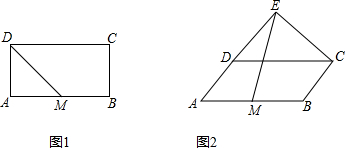
(2)如图2,若四边形ABCD是平行四边形,AB=2BC,M是AB的中点,过C作CE⊥AD与AD所在直线交于点E.
①若∠A为锐角,则∠BME与∠AEM有怎样的倍数关系,并证明你的结论;
②当0°<∠A<
120
120
°时,上述结论成立;当120
120
°≤∠A<180°时,上述结论不成立.
分析:(1)求出AM=AD,得到△ADM是等腰直角三角形,然后求出∠BMD与∠ADM的度数,从而得解;
(2)①连接CM,取CE的中点F,连接MF,交DC于N,根据平行线分线段成比例定理可得MF∥AE∥BC,再根据两直线平行,内错角相等可得∠AEM=∠1,∠2=∠4,再根据AB=2BC,M是AB的中点,利用等边对等角的性质求出∠3=∠4,根据三角形三线合一的性质求出∠1=∠2,从而得解;
②求出当点E与点A重合时的∠A的度数,即为临界值,小于临界值,点E在射线AD上,成立,否则不成立.
(2)①连接CM,取CE的中点F,连接MF,交DC于N,根据平行线分线段成比例定理可得MF∥AE∥BC,再根据两直线平行,内错角相等可得∠AEM=∠1,∠2=∠4,再根据AB=2BC,M是AB的中点,利用等边对等角的性质求出∠3=∠4,根据三角形三线合一的性质求出∠1=∠2,从而得解;
②求出当点E与点A重合时的∠A的度数,即为临界值,小于临界值,点E在射线AD上,成立,否则不成立.
解答:解:(1)∵AB=2BC,M是AB的中点,
∴AD=BC=AM,
∴△ADM是等腰直角三角形,
∴∠ADM=45°,∠BMD=180°-∠AMD=180°-45°=135°,
∴∠BMD=3∠ADM;
(2)①如图,连接CM,取CE的中点F,连接MF,交DC于N,
∵M是AB的中点,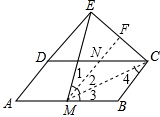
∴MF∥AE∥BC,
∴∠AEM=∠1,∠2=∠4,
∵AB=2BC,
∴BM=BC,
∴∠3=∠4.
∵CE⊥AE,
∴MF⊥EC,
又∵F是EC的中点,
∴ME=MC,
∴∠1=∠2,
∴∠1=∠2=∠3,
∴∠BME=3∠AEM;
②当点E与点A重合时,∵CE⊥AD,AB=2BC,
∴∠B=60°,
∴∠A=180°-∠B=180°-60°=120°,
所以,当0°<∠A<120°时,结论成立;
当120°≤∠A<180°时,结论不成立.
∴AD=BC=AM,
∴△ADM是等腰直角三角形,
∴∠ADM=45°,∠BMD=180°-∠AMD=180°-45°=135°,
∴∠BMD=3∠ADM;
(2)①如图,连接CM,取CE的中点F,连接MF,交DC于N,
∵M是AB的中点,

∴MF∥AE∥BC,
∴∠AEM=∠1,∠2=∠4,
∵AB=2BC,
∴BM=BC,
∴∠3=∠4.
∵CE⊥AE,
∴MF⊥EC,
又∵F是EC的中点,
∴ME=MC,
∴∠1=∠2,
∴∠1=∠2=∠3,
∴∠BME=3∠AEM;
②当点E与点A重合时,∵CE⊥AD,AB=2BC,
∴∠B=60°,
∴∠A=180°-∠B=180°-60°=120°,
所以,当0°<∠A<120°时,结论成立;
当120°≤∠A<180°时,结论不成立.
点评:本题考查了矩形的性质,平行四边形的性质以及平行线的性质,(2)比较复杂,作出辅助线,把∠BME分成相等的三个角是解题的关键.

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
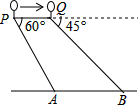 (2013•葫芦岛)如图,一热气球在距地面90米高的P处,观测地面上点A的俯角为60°,气球以每秒9米的速度沿AB方向移动,5秒到达Q处,此时观测地面上点B的俯角为45°.(点P,Q,A,B在同一铅直面上).
(2013•葫芦岛)如图,一热气球在距地面90米高的P处,观测地面上点A的俯角为60°,气球以每秒9米的速度沿AB方向移动,5秒到达Q处,此时观测地面上点B的俯角为45°.(点P,Q,A,B在同一铅直面上).