题目内容
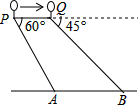 (2013•葫芦岛)如图,一热气球在距地面90米高的P处,观测地面上点A的俯角为60°,气球以每秒9米的速度沿AB方向移动,5秒到达Q处,此时观测地面上点B的俯角为45°.(点P,Q,A,B在同一铅直面上).
(2013•葫芦岛)如图,一热气球在距地面90米高的P处,观测地面上点A的俯角为60°,气球以每秒9米的速度沿AB方向移动,5秒到达Q处,此时观测地面上点B的俯角为45°.(点P,Q,A,B在同一铅直面上).(1)若气球从Q处继续向前移动,方向不变,再过几秒位于B点正上方?
(2)求AB的长(结果保留根号).
分析:(1)首先过点B作BH⊥PQ,垂足为H,即可得出QH=HB=90m,进而利用平移速度得出答案;
(2)首先过点P作PE⊥AB,垂足为E,利用tan60°=
=
=
,进而得出AE的长,再利用PH=BE进而得出AB的长.
(2)首先过点P作PE⊥AB,垂足为E,利用tan60°=
| PE |
| AE |
| 90 |
| AE |
| 3 |
解答: 解:(1)过点B作BH⊥PQ,垂足为H,
解:(1)过点B作BH⊥PQ,垂足为H,
∵一热气球在距地面90米高的P处,
∴HB=90m,
∵∠HQB=45°,
∴∠2=45°,
∴QH=HB=90m,
∴90÷9=10(秒),
答:气球从Q处继续向前移动,方向不变,再过10秒位于B点正上方;
(2)过点P作PE⊥AB,垂足为E,
∵一热气球在距地面90米高的P处,
∴PE=90m,
∵∠QPA=60°,
∴∠1=60°,
∴tan60°=
=
=
,
∴AE=
=30
,
∵气球以每秒9米的速度沿AB方向移动,5秒到达Q处,
∴PQ=5×9=45(m),
∴PH=45+90=135(m),
∴BE=135(m),
∴AB=BE-AE=(135-30
)m,
答:AB的长为(135-30
)m.
 解:(1)过点B作BH⊥PQ,垂足为H,
解:(1)过点B作BH⊥PQ,垂足为H,∵一热气球在距地面90米高的P处,
∴HB=90m,
∵∠HQB=45°,
∴∠2=45°,
∴QH=HB=90m,
∴90÷9=10(秒),
答:气球从Q处继续向前移动,方向不变,再过10秒位于B点正上方;
(2)过点P作PE⊥AB,垂足为E,
∵一热气球在距地面90米高的P处,
∴PE=90m,
∵∠QPA=60°,
∴∠1=60°,
∴tan60°=
| PE |
| AE |
| 90 |
| AE |
| 3 |
∴AE=
| 90 | ||
|
| 3 |
∵气球以每秒9米的速度沿AB方向移动,5秒到达Q处,
∴PQ=5×9=45(m),
∴PH=45+90=135(m),
∴BE=135(m),
∴AB=BE-AE=(135-30
| 3 |
答:AB的长为(135-30
| 3 |
点评:此题主要考查了仰角与俯角的应用,根据题意得出直角三角形利用已知角度得出HQ的长是解题关键.

练习册系列答案
相关题目
 (2013•葫芦岛)如图,AB是半圆的直径,AB=2,∠B=30°,则
(2013•葫芦岛)如图,AB是半圆的直径,AB=2,∠B=30°,则
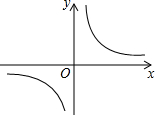 (2013•葫芦岛)如图是反比例函数y=
(2013•葫芦岛)如图是反比例函数y=