Question

【题目】如图，在平面直角坐标系中，直线y=-x+b分别与x轴、y轴交于点A、B，且点A的坐标为（4，0），四边形ABCD是正方形．

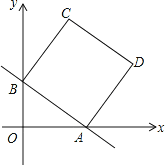
（1）填空：b= ；

（2）求点D的坐标；

（3）点M是线段AB上的一个动点（点A、B除外），试探索在x上方是否存在另一个点N，使得以O、B、M、N为顶点的四边形是菱形？若不存在，请说明理由；若存在，请求出点N的坐标．

Answer 1

【答案】（1）3;（2） 点N的坐标为（-2，）、（，）．．

【解析】

试题分析：（1）把（4，0）代入y=-x+b即可求得b的值；

（2）过点D作DE⊥x轴于点E，证明△OAB≌△EDA，即可求得AE和DE的长，则D的坐标即可求得；

（3）分当OM=MB=BN=NO时；当OB=BN=NM=MO=3时两种情况进行讨论．

试题解析：（1）把（4，0）代入y=-x+b，得：-3+b=0，解得：b=3，

（2）如图1，过点D作DE⊥x轴于点E，

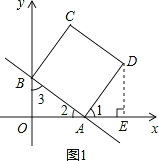
∵正方形ABCD中，∠BAD=90°，

∴∠1+∠2=90°，

又∵直角△OAB中，∠1+∠2=90°，

∴∠1=∠3，

在△OAB和△EDA中，

，

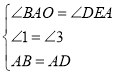∴△OAB≌△EDA，

∴AE=OB=3，DE=OA=4，

∴OE=4+3=7，

∴点D的坐标为（7，4）；

（3）存在．

①如图2，当OM=MB=BN=NO时，四边形OMBN为菱形．

则MN在OB的中垂线上，则M的纵坐标是，

把y=代入y=-x+4中，得x=2，即M的坐标是（2，），

则点N的坐标为（-2，）．

②如图3，当OB=BN=NM=MO=3时，四边形BOMN为菱形．

∵ON⊥BM，

∴ON的解析式是y=x．

根据题意得：

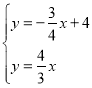，解得：．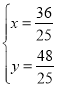

则点N的坐标为（，）．