题目内容
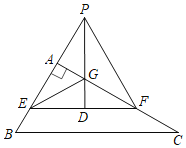
【题目】在Rt△ABC中,∠BAC=90°,E,F分别是AB,AC上的点,且EF∥BC,作EG平分∠AEF交AC于点G,在EF上取点D,使ED=EA,连接DG并延长,交BA的延长于点P,连接PF.
(1)求证:PD⊥EF;
(2)若ED=DF,求∠B的大小.
(3)在(2)的条件下,若四边形AEDG的面积为S,请直接写出△PEF的面积(用含S的式子表示).
【答案】(1)详见解析;(2)60°;(3)S△PEF=3S.
【解析】
(1)由“SAS”可证△AEG≌△DEG,可得∠GAE=∠GDE=90°,可得PD⊥EF;
(2)由线段垂直平分线的性质可得EG=GF,可得∠GFE=∠GEF,由直角三角形的性质可求∠AEG=∠GEF=∠GFE=30°,由平行线的性质可求解;
(3)先证△PEF是等边三角形,可证四边形AEDG的面积=![]() S△AEF=
S△AEF=![]() S△PEF,即可求解.
S△PEF,即可求解.
(1)∵EG平分∠AEF,
∴∠AEG=∠DEG,
在△AEG和△DEG中,
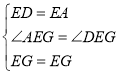 ,
,
∴△AEG≌△DEG(SAS)
∴∠GAE=∠GDE=90°,
∴PD⊥EF;
(2)∵ED=DF,PD⊥EF,
∴EG=GF,
∴∠GFE=∠GEF,
∴∠AEG=∠GEF=∠GFE,
∵∠AEG+∠GEF+∠GFE=90°,
∴∠AEG=∠GEF=∠GFE=30°,
∴∠AEF=60°,
∵EF∥BC,
∴∠AEF=∠B=60°
(2)∵ED=DF,PD⊥EF,
∴PE=PF,且∠PEF=60°,
∴△PEF是等边三角形,
∵AF⊥AB,
∴AE=AP,
∴S△AEF=S△AFP,
∵∠BAC=90°,∠AEG=30°,
∴EG=2AG,
∴GF=2AG,
∴2S△AEG=S△EGF,
∵ED=DF,
∴S△GED=S△GFD,
∴S△GED=S△GFD=S△AEG,
∴四边形AEDG的面积=![]() S△AEF=
S△AEF=![]() S△PEF,
S△PEF,
∴S△PEF=3S.