Question

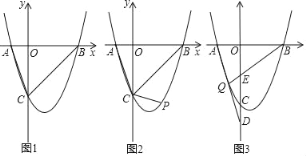
【题目】如图1，已知矩形AOCB，AB＝6cm，BC＝16cm，动点P从点A出发，以3cm/s的速度向点O运动，直到点O为止；动点Q同时从点C出发，以2cm/s的速度向点B运动，与点P同时结束运动．

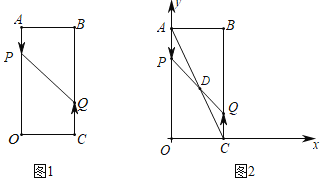
(1)当出发　 　时，点P和点Q之间的距离是10cm；

(2)逆向发散：当运动时间为2s时，P、Q两点的距离为　 　cm；当运动时间为4s时，P、Q两点的距离为　 　cm；

(3)探索发现：如图2，以点O为坐标原点，OC所在直线为x轴，OA所在直线为y轴，1cm长为单位长度建立平面直角坐标系，连接AC，与PQ相交于点D，若双曲线y＝过点D，问k的值是否会变化？若会变化，说明理由；若不会变化，请求出k的值．

Answer 1

【答案】（1）s或s；（2）6，2；（3）不会变化，k＝．

【解析】

（1）作PH⊥BC，根据勾股定理求出QH，分点H在BQ之间、点H在CQ之间两种情况计算；

（2）根据题意分别求出QH的长，根据勾股定理计算，得到答案；

（3）作DE⊥AO于点E，根据相似三角形的性质得到，证明△AED∽△AOC，根据相似三角形的性质求出点D的坐标，得到k的值．

解：（1）作PH⊥BC于点H，则四边形APHB为矩形，

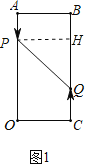
∴PH＝AB＝6，BH＝AP＝3t，

当PQ＝10时，由勾股定理得，QH＝，

当点H在BQ之间时，QH＝BC﹣BH﹣CQ＝16﹣5t，

则16﹣5t＝8，

解得，t＝，

当点H在CQ之间时，QH＝CQ﹣（BC﹣BH）＝5t﹣16，

则5t﹣18＝8，

解得，t＝，

则当t＝s或s时，点P和点Q之间的距离是10cm，

故答案为：s或s；

（2）当t＝2s时，QH＝16﹣5t＝6，

则PQ＝＝，

当当t＝4s时，QH＝5t﹣16＝4，

则PQ＝，

故答案为：；；

（3）k的值不会变化，

理由如下：作DE⊥AO于点E，

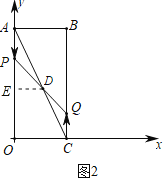
∵OA∥BC，

∴△ADP∽△CDQ，

∴，

∵DE⊥AO，∠AOC＝90°，

∴DE∥OC，

∴△AED∽△AOC，

∴，即，

解得，AE＝，DE＝，

∴OE＝AO﹣AE＝，

∴点D的坐标为（，），

则k＝×＝．