题目内容
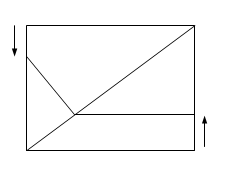
如图,四边形ABCD为矩形,AB=4,AD=3,动点M、N分别从D、B同时出发,以1个单位/秒的速度运动,点M沿DA向终点A运动,点N沿BC向终点C运动。过点N作NP⊥BC,交AC于点P,连结MP。已知动点运动了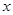 秒。
秒。
小题1:请直接写出PN的长 ;(用含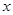 的代数式表示)
的代数式表示)
小题2:若0秒≤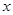 ≤3秒,试求△MPA的面积S与时间
≤3秒,试求△MPA的面积S与时间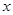 秒的函数关系式,并求S的最大值。
秒的函数关系式,并求S的最大值。
小题3:若0秒≤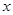 ≤3秒,△MPA能否与△PCN相似?若能,试求出相似时
≤3秒,△MPA能否与△PCN相似?若能,试求出相似时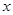 的对应值;若不能,试说明理由。
的对应值;若不能,试说明理由。
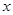 秒。
秒。
小题1:请直接写出PN的长 ;(用含
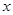 的代数式表示)
的代数式表示)小题2:若0秒≤
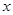 ≤3秒,试求△MPA的面积S与时间
≤3秒,试求△MPA的面积S与时间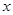 秒的函数关系式,并求S的最大值。
秒的函数关系式,并求S的最大值。小题3:若0秒≤
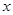 ≤3秒,△MPA能否与△PCN相似?若能,试求出相似时
≤3秒,△MPA能否与△PCN相似?若能,试求出相似时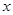 的对应值;若不能,试说明理由。
的对应值;若不能,试说明理由。小题1:
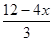 ;
;小题2:延长NP交AD于点Q,则PQ⊥AD,由⑴得:PN=
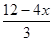 ,
,则
 。
。依题意,可得:
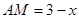
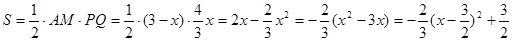 ∵0≤
∵0≤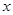 ≤1.5
≤1.5 ∴当
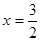 时,S有最大值,S最大值=
时,S有最大值,S最大值=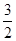 。…………………4分
。…………………4分小题3:能相似
共有两种情况,以下分类说明:
①
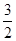 …………………2分
…………………2分②3或
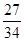 …………………2分
…………………2分综上所述,当
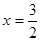 ,或
,或 ,或
,或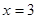 时,△MPA与△NPA相似
时,△MPA与△NPA相似(1)可在直角三角形CPN中,根据CN的长和∠CPN的正切值求出.
(2)三角形MPA中,底边AM的长为3-x,关键是求出MA边上的高,可延长NP交AD于Q,那么PQ就是三角形AMP的高,可现在直角三角形CNP中求出PN的长,进而根据AB的长,表示出PQ的长,根据三角形的面积公式即可得出S与x的函数关系式.根据函数的性质可得出S的最大值.
(3)本题要分三种情况:
①MP=PA,那么AQ=BN=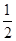 AM,可用x分别表示出BN和AM的长,然后根据上述等量关系可求得x的值.
AM,可用x分别表示出BN和AM的长,然后根据上述等量关系可求得x的值.
②MA=MP,在直角三角形MQP中,MQ=MA-BN,PQ=AB-PN根据勾股定理即可求出x的值.
③MA=PA,不难得出AP=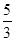 BN,然后用x表示出AM的长,即可求出x的值.
BN,然后用x表示出AM的长,即可求出x的值.
(2)三角形MPA中,底边AM的长为3-x,关键是求出MA边上的高,可延长NP交AD于Q,那么PQ就是三角形AMP的高,可现在直角三角形CNP中求出PN的长,进而根据AB的长,表示出PQ的长,根据三角形的面积公式即可得出S与x的函数关系式.根据函数的性质可得出S的最大值.
(3)本题要分三种情况:
①MP=PA,那么AQ=BN=
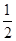 AM,可用x分别表示出BN和AM的长,然后根据上述等量关系可求得x的值.
AM,可用x分别表示出BN和AM的长,然后根据上述等量关系可求得x的值.②MA=MP,在直角三角形MQP中,MQ=MA-BN,PQ=AB-PN根据勾股定理即可求出x的值.
③MA=PA,不难得出AP=
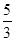 BN,然后用x表示出AM的长,即可求出x的值.
BN,然后用x表示出AM的长,即可求出x的值.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 cm,
cm, cm,
cm,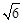 cm
cm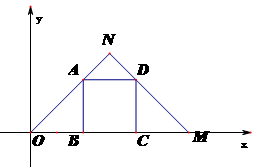

 摄制组在拍摄中心C出发,乘船到达码头B后,立即返回.求船只往返B、C两处所用的时间.
摄制组在拍摄中心C出发,乘船到达码头B后,立即返回.求船只往返B、C两处所用的时间.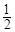 AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC.
AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC.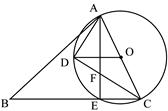
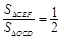 ,且AC=4,求CF的长.
,且AC=4,求CF的长.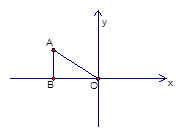
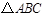 与
与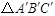 是位似图形,点
是位似图形,点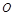 是位似中心,若OA=2AA′,S△ABC=8,则
是位似中心,若OA=2AA′,S△ABC=8,则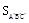 =( )
=( )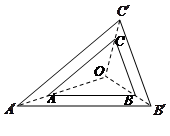
 在方格纸中
在方格纸中
 ,并求出
,并求出 点坐标;
点坐标; 为位似中心,相似比为2,在第一象限内将
为位似中心,相似比为2,在第一象限内将 ;
;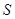 .
.