题目内容
【题目】如图,抛物线y=﹣x2+bx+c经过直线y=﹣x+3与坐标轴的两个交点A、B,与x轴的另一个交点为C,顶点为D.
(1)求抛物线的解析式;
(2)画出抛物线的图象;
(3)在x轴上是否存在点N使△ADN为直角三角形?若存在,求出点N的坐标;若不存在,请说明理由.
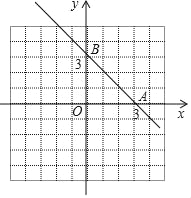
【答案】(1)抛物线的解析式为y=﹣x2+2x+3.(2)图象见解析;(3)点N的坐标为(1,0)或(﹣7,0).
【解析】
(1)先求得点A和点B的坐标,然后将点A和点B的坐标代入抛物线的解析式求得b,c的值即可;
(2)依据抛物线解析式为y=-x2+2x+3,列表,描点,连线即可;
(3)先利用配方法求得点D的坐标,当∠DNA=90°时,DN⊥OA,可得到点N的坐标,从而得到AN=2,然后再求得AD的长;当∠N′DA=90°时,依据sin∠DN′A=sin∠ADN可求得AN′的长,从而可得到N′的坐标.
解:(1)将x=0代入AB的解析式y=﹣x+3得:y=3,
∴B(0,3).
将y=0代入AB的解析式y=﹣x+3得:﹣x+3=0,
解得x=3,
即A(3,0).
将点A和点B的坐标代入y=﹣x2+bx+c,得:
![]() ,
,
解得:b=2,c=3.
∴抛物线的解析式为y=﹣x2+2x+3.
(2)列表:
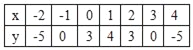
抛物线的图象如下:
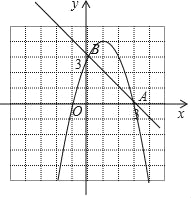
(3)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴D(1,4).
①当∠DNA=90°时,如图所示:
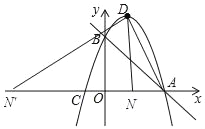
∵∠DNA=90°时,
∴DN⊥OA.
又∵D(1,4)
∴N(1,0).
∴AN=2.
∵DN=4,AN=2,
∴AD=2![]() .
.
②当∠N′DA=90°时,则∠DN′A=∠NDA.
∴![]() ,
,
即![]() ,
,
解得:AN′=10.
∵A(3,0),
∴N′(﹣7,0).
综上所述,点N的坐标为(1,0)或(﹣7,0).

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目