Ő‚ńŅńŕ»›
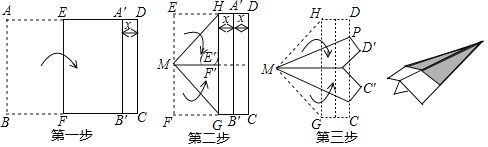
°ĺŐ‚ńŅ°Ņ£®1£©≥Ę ‘ŐĹĺŅ
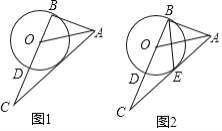
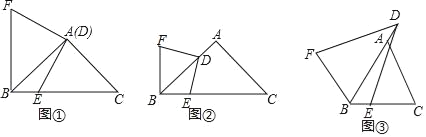
»ÁÕľ1£¨Ķ»—ŁRt°ųABCĶńŃĹłŲ∂•Ķ„B£¨C‘ŕ÷ĪŌŖMN…Ō£¨Ķ„D «÷ĪŌŖMN…Ō“ĽłŲ∂ĮĶ„£®Ķ„D‘ŕĶ„CĶń”“ĪŖ£©£¨BC=3£¨BD=m£¨‘ŕ°ųABCÕ¨≤ŗ◊ųĶ»—ŁRt°ųADE£¨°ŌABC=°ŌADE=90°„£¨EF°Õ MN”ŕĶ„F£¨Ń¨ĹŠCE.
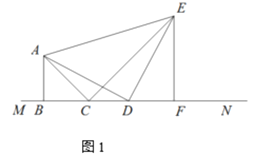
ĘŔ«ůDFĶń≥§£Ľ
Ęŕ‘ŕŇ–∂ŌAC°ÕCE «∑Ů≥…ŃĘ Ī£¨–°√ųÕ¨—ß∑ĘŌ÷Ņ…“‘”…“‘Ō¬ŃĹ÷÷ňľ¬∑Ĺ‚ĺŲīňő Ő‚£ļ
ňľ¬∑“Ľ£ļŌ»÷§CF=EF£¨«ů≥Ų°ŌECF=45°„£¨ī”∂Ý÷§Ķ√ĹŠ¬Ř≥…ŃĘ.
ňľ¬∑∂Ģ£ļŌ»«ůDF£¨EFĶń≥§£¨‘Ŕ«ůCFĶń≥§£¨»Ľļů÷§AC2+CE2=AE2£¨ī”∂Ý÷§Ķ√ĹŠ¬Ř≥…ŃĘ.
«Žń„»ő—°“Ľ÷÷ňľ¬∑£¨ÕÍ’ŻĶō ť–īĪĺ–°Ő‚Ķń÷§√ųĻż≥Ő.(»Á”√ŃĹ÷÷∑Ĺ∑®◊ųīū£¨‘Ú“‘Ķŕ“Ľ÷÷∑Ĺ∑®∆ņ∑÷)
£®2£©Õō’ĻŐĹĺŅ
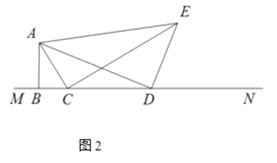
Ĺę(1)÷–ĶńŃĹłŲĶ»—Ł÷ĪĹ«»żĹ«–ő∂ľłńő™”–“ĽłŲĹ«ő™Ķń÷ĪĹ«»żĹ«–ő£¨»ÁÕľ2£¨ °ŌABC=°ŌADE=90°„£¨°ŌBAC=°ŌDAE=30°„£¨BC=3£¨BD=m£¨ĶĪ4°‹m°‹6 Ī£¨«ůCE≥§Ķń∑∂őß.
°ĺīūįł°Ņ£®1£©ĘŔ3£ĽĘŕŌÍľŻĹ‚őŲ£Ľ£®2£©![]() .
.
°ĺĹ‚őŲ°Ņ
£®1£©ĘŔ÷§√ų°ųABD°’ °ųDFEľīŅ…Ķ√≥ŲĹŠ¬Ř£Ľ
Ęŕňľ¬∑“Ľ£ļŌ»÷§CF=EF£¨«ů≥Ų°ŌECF=45°„£¨ī”∂Ý÷§Ķ√ĹŠ¬Ř≥…ŃĘ.
ňľ¬∑∂Ģ£ļŌ»«ůDF£¨EFĶń≥§£¨‘Ŕ«ůCFĶń≥§£¨»Ľļů÷§AC2+CE2=AE2£¨ī”∂Ý÷§Ķ√ĹŠ¬Ř≥…ŃĘ.
£®2£©“◊÷§°ų ABD °◊°ų DFE£¨Ķ√![]() £¨Ņ…«ů≥ŲCF= m£¨CE=
£¨Ņ…«ů≥ŲCF= m£¨CE=![]() £¨Ķ√°ŌACE=90°„£¨ňý“‘őř¬Řm»°ļőīů”ŕ3Ķń ż£¨AC°ÕCE◊‹≥…ŃĘ£¨ľīĶ„E‘ŕ“ĽŐű÷ĪŌŖ…Ō‘ň∂Į£¨“ÚīňŅ…«ů≥ŲĶĪ4°‹m°‹6 Ī£¨CE≥§Ķń∑∂őß.
£¨Ķ√°ŌACE=90°„£¨ňý“‘őř¬Řm»°ļőīů”ŕ3Ķń ż£¨AC°ÕCE◊‹≥…ŃĘ£¨ľīĶ„E‘ŕ“ĽŐű÷ĪŌŖ…Ō‘ň∂Į£¨“ÚīňŅ…«ů≥ŲĶĪ4°‹m°‹6 Ī£¨CE≥§Ķń∑∂őß.
£®1£©ĘŔ‘ŕĶ»—ŁRt°ųABCļÕĶ»—ŁRt°ųADE÷–£¨°ŌABC=°ŌADE=90°„£¨°ŗ°ŌADB+°ŌEDF=90°„£¨
°ŖEF°Õ MN£¨
°ŗ°ŌDEF+°ŌEDF=90°„£¨
°ŗ°ŌADB=°ŌDEF£¨
‘ŕ°ųABDļÕ°ųDFE÷–£¨

°ŗ°ųABD°’ °ųDFE£®AAS£©£¨
°ŗDF=AB=BC=3£Ľ
Ęŕ÷§√ų£ļňľ¬∑“Ľ£ļ
”…ĘŔĶ√°ųABD°’ °ųDFE£®AAS£©£¨
°ŗDF=AB=BC=3£¨EF=BD=m£¨
°ŗCF=CD+DF=CD+BC=BD=m£¨
°ŗCF=EF£¨
°ŖEF°Õ MN£¨
°ŗ°ŌECF=45°„£¨
°Ŗ°ŌACB=45°„£¨
°ŗ°ŌACE=90°„£¨
ľīAC°ÕCE£Ľ
ňľ¬∑∂Ģ£ļ”…£®1£©÷™£¨DF=AB=3£¨EF=BD=3+m
°ŗDE=AD=![]()
°ŗAE=![]()
”÷”…£®1£©Ņ…÷™£¨°ŌEFD=°ŌABC=90°„,CF=EF=3+m£¨
°ŗAC=3![]() ,CE=(3+m)
,CE=(3+m) ![]()
°ŖAC2+CE2=![]() = AE2£¨
= AE2£¨
°ŗ°ųACE «÷ĪĹ«»żĹ«–ő£¨ľīAC°ÕCE£Ľ
£®2£©»ÁÕľ£¨◊ųEF°Õ MN£¨

°ŗ°ŌDEF+°ŌEDF=90°„£¨
°Ŗ°ŌADE=90°„£¨
°ŗ°ŌADB+°ŌEDF=90°„£¨
°ŗ°ŌADB=°ŌDEF£¨
°ŗ°ų ABD °◊°ų DFE£¨
°ŗ![]() £¨
£¨
°ŗEF=![]() £¨DF=3£¨
£¨DF=3£¨
°ŗCF=CD+DF=CD+BC=BD=m£¨
°ŗ‘ŕRt°ųCEF÷–£¨tan°ŌECF=![]() ,
,
°ŗ°ŌECF=30°„£¨CE=2EF=![]() £¨
£¨
°ŗ°ŌACE=90°„£¨
ľīAC°ÕCE£¨
°ŗőř¬Řm»°ļőīů”ŕ3Ķń ż£¨AC°ÕCE◊‹≥…ŃĘ£¨ľīĶ„E‘ŕ“ĽŐű÷ĪŌŖ…Ō‘ň∂Į£¨
°ŗ4°‹m°‹6 Ī£¨CE≥§Ķń∑∂őß «![]() .
.

 √Ņ»’10∑÷÷”Ņŕň„–ńň„ňŔň„ŐžŐžŃ∑ŌĶŃ–īūįł
√Ņ»’10∑÷÷”Ņŕň„–ńň„ňŔň„ŐžŐžŃ∑ŌĶŃ–īūįł