Question

【题目】如图所示,用火柴杆摆出一系列三角形图案,共摆有n层，当n=1时，需3火柴；当n=2时，需9根火柴，按这种方式摆下去,

（1）当n=3时，需 根火柴．

（2）当n=20时，需 根火柴．

（3）用含n的式子写出规律来______________________________

Answer 1

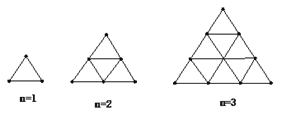
【答案】(1)18 (2) 630 (3) 3(1+n)n/2

【解析】试题分析：（1）观察图形即可得出；

（2）设第n个三角形图案需要的火柴棍数为an（n为正整数）根，根据给定图形找出部分an的值，根据数的变化找出变化规律“an=”，依此规律即可得出结论；

（2）根据（1）中规律解答即可．

试题解析：（1）n=1时，有1个三角形，需要火柴的根数为3×1；

n=2时，有5个三角形，需要火柴的根数为3×(1+2)；

n=3时，需要火柴的根数为3×(1+2+3)=18，

故答案为：18；

（2）根据（1）中的规律，当n=10时，需要火柴的根数为3×(1+2+3+…+20)=210，

故答案为：210；

（3）根据上述规律可得：3×(1+2+3+…+n)= .