题目内容
(2012•密云县一模)在∠A(0°<∠A<90°)的内部画线段,并使线段的两端点分别落在角的两边AB、AC上,如图所示,从点A1开始,依次向右画线段,使线段与线段在两端点处互相垂直,A1A2为第1条线段.设AA1=A1A2=A2A3=1,则∠A=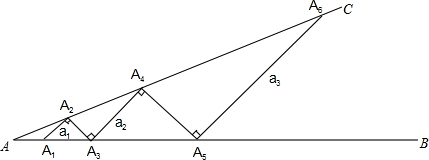
22.5
22.5
°;若记线段A2n-1A2n的长度为an(n为正整数),如A1A2=a1,A3A4=a2,则此时a2=1+
| 2 |
1+
,an=| 2 |
(1+
)n-1
| 2 |
(1+
)n-1
(用含n的式子表示).| 2 |

分析:由题意得到△A1A2A3为等腰直角三角形,利用等腰直角三角形的性质得到∠A2A1A3=45°,再由∠A2A1A3为等腰△AA2A1的外角,利用外角性质即可求出∠A的度数;由△A1A2A3为等腰直角三角形,A1A2=A2A3=1,利用勾股定理求出A1A3的长,由AA1+A1A3求出AA3的长,即为A3A4的长,可得出a2的长;同理求出a3的长,依此类推即可得出an的长.
解答:解:∵A1A2=A2A3,A1A2⊥A2A3,
∴△A1A2A3为等腰直角三角形,
∴∠A2A1A3=45°,
又AA1=A1A2,
∴∠A=∠AA2A1,
又∠A2A1A3为△AA2A1的外角,
∴∠A=∠AA2A1=
∠A2A1A3=22.5°;
∵AA1=A1A2=A2A3=1,
∴A1A2=a1=1;
在Rt△A1A2A3中,根据勾股定理得:A1A3=
,
∴AA3=A3A4=a2=AA1+A1A3=1+
;
同理AA5=A5A6=a3=AA3+A3A5=1+
+
(1+
)=3+2
=(1+
)2;
以此类推,an=(1+
)n-1.
故答案为:22.5°;1+
;(1+
)n-1.
∴△A1A2A3为等腰直角三角形,
∴∠A2A1A3=45°,
又AA1=A1A2,
∴∠A=∠AA2A1,
又∠A2A1A3为△AA2A1的外角,
∴∠A=∠AA2A1=
| 1 |
| 2 |
∵AA1=A1A2=A2A3=1,
∴A1A2=a1=1;
在Rt△A1A2A3中,根据勾股定理得:A1A3=
| 2 |
∴AA3=A3A4=a2=AA1+A1A3=1+
| 2 |
同理AA5=A5A6=a3=AA3+A3A5=1+
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
以此类推,an=(1+
| 2 |
故答案为:22.5°;1+
| 2 |
| 2 |
点评:此题考查了等腰直角三角形的性质,勾股定理,以及三角形的外角性质,属于规律型题,锻炼了学生归纳总结的能力,是中考中常考的题型.

练习册系列答案
相关题目
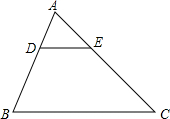 (2012•密云县一模)如图,在△ABC中,DE∥BC,AD=2,AB=6,DE=3,则BC的长为( )
(2012•密云县一模)如图,在△ABC中,DE∥BC,AD=2,AB=6,DE=3,则BC的长为( )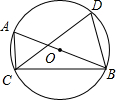 (2012•密云县一模)如图,△ABC内接于⊙O,AB是⊙O的直径,∠ABC=20°,点D是弧CAB上一点,若∠ABC=20°,则∠D的度数是
(2012•密云县一模)如图,△ABC内接于⊙O,AB是⊙O的直径,∠ABC=20°,点D是弧CAB上一点,若∠ABC=20°,则∠D的度数是