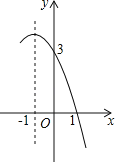题目内容
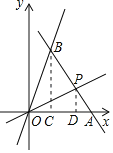
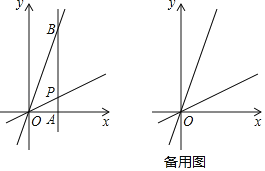
【题目】在平面直角坐标系xOy中,第一象限内的点P在直线y=![]() x上,过点P的直线交x轴正半轴于点A,交直线y=3x于点B,点B在第一象限内.
x上,过点P的直线交x轴正半轴于点A,交直线y=3x于点B,点B在第一象限内.
(1)如图1,当∠OAB=90°时,求![]() 的值;
的值;
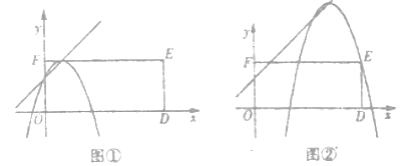
(2)当点A的坐标为(6,0),且BP=2AP时,将过点A的抛物线y=﹣x2+mx上下方平移,使它过点B,求平移的方向和距离.
【答案】(1)5;(2)抛物线向下平移了![]() 个单位长度.
个单位长度.
【解析】
(1)设点A横坐标为a,由于∠OAB=90°,即AB⊥x轴,所以P、B横坐标也是a,分别代入直线解析式求P、B纵坐标,相减即能得到用a表示的BP、AP的值.
(2)分别过点P、B作x轴垂线,垂足分别为D、C,根据平行线分线段定理可得![]() .设直线AB解析式为y=kx+b,把A坐标代入得y=kx﹣6k.把直线AB解析式分别与直线OP、OB解析式联立方程组,求得点P、B的横坐标(用k表示)即点D、C横坐标,进而得到用k表示CD、DA的式子.根据CD=2AD为等量关系列方程即求得k的值,即得到点B坐标.把点A代入原抛物线解析式求m,由于上下平移,故可在原抛物线解析式后+n以表示平移后的抛物线,把点B代入即求得n的值.n为负数时即表示向下平移.
.设直线AB解析式为y=kx+b,把A坐标代入得y=kx﹣6k.把直线AB解析式分别与直线OP、OB解析式联立方程组,求得点P、B的横坐标(用k表示)即点D、C横坐标,进而得到用k表示CD、DA的式子.根据CD=2AD为等量关系列方程即求得k的值,即得到点B坐标.把点A代入原抛物线解析式求m,由于上下平移,故可在原抛物线解析式后+n以表示平移后的抛物线,把点B代入即求得n的值.n为负数时即表示向下平移.
(1)设点A坐标为(a,0)(a>0)
∵∠OAB=90°,点B在直线y=3x上,点P在直线y=![]() x上
x上
![]()
![]()
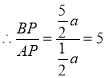 (2)如图,过点B作BC⊥x轴于点C,过点P作PD⊥x轴于点D
(2)如图,过点B作BC⊥x轴于点C,过点P作PD⊥x轴于点D
∴BC∥PD
∵BP=2AP
∴![]() =2
=2
∴CD=2DA
设直线AB解析式为:y=kx+b
∵A(6,0)
∴6k+b=0,得b=﹣6k
∴直线AB解析式为y=kx﹣6k
当![]() x=kx﹣6k时,解得:x=
x=kx﹣6k时,解得:x=![]()
∴xD=xP=![]()
当3x=kx﹣6k时,解得:x=![]()
![]()
![]()
![]() 解得:k=﹣2
解得:k=﹣2
∴![]() ,即
,即![]()
∵抛物线y=﹣x2+mx过点A
∴﹣36+6m=0,解得:m=6
设平移后过点B的抛物线解析式为y=﹣x2+6x+n
∴
解得:n=﹣![]()
∴抛物线向下平移了![]() 个单位长度.
个单位长度.