题目内容
在△ABC中,点D、E分别在边AB、AC上,如果AD=1,BD=2,那么由下列条件能够判断DE∥BC的是( )
(A) (B)
(B)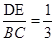 ; (C)
; (C) ; (D)
; (D) 。
。
D.
解析试题分析:根据相似三角形的判定得出△ADE∽△ABC即可推出∠ADE=∠B,根据平行线的判定推出即可.
∵AD=1,BD=2,
∴AD:AB=1:3,
只有当AE:AC=1:3时,DE∥BC,
理由是:∵AD:AB=AE:AC=1:3,∠A=∠A,
∴△ADE≌△ABC,
∴∠ADE=∠B,
∴DE∥BC,
而其它选项都不能推出∠ADE=∠B或∠AED=∠C,即不能推出DE∥BC,
即选项A、B、C都错误,只有选项D正确;
考点:平行线分线段成比例.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
如图,在△ABC中,DE∥BC,若AD:AB=1:3,则△ADE与△ABC的面积之比是
| A.1:3 | B.1:4 | C.1:9 | D.1:16 |
如图,身高为1.5米的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3米,CA=1米,则树的高度为( )
| A.3米 | B.4米 | C.4.5米 | D.6米 |
在平行四边形ABCD中,点E在AD上,且AE:ED=3:1,CE的延长线与BA的延长线交于点F,则S△AFE:S四边形ABCE为( )
| A.3:4 | B.4:3 | C.7:9 | D.9:7 |
如图,O为矩形ABCD的中心,将直角三角板的直角顶点与O点重合,转动三角板使两直角边始终与BC,AB相交,交点分别为M,N.如果AB=4,AD=6,OM=x,ON=y.则y与x的关系是( )
A. | B. | C.y=x | D. |
已知等边△ 中,
中, ,
, 与
与 相交于点
相交于点 ,则∠
,则∠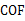 等于( )
等于( )
| A.75° | B.60° | C.55° | D.45° |

 ,点
,点 是线段
是线段 上任意一点,点
上任意一点,点 是线段
是线段 的中点,点
的中点,点 是线段
是线段 的中点,求线段
的中点,求线段 的长.
的长.
