题目内容
【题目】探究:
(1)如图①,在等腰直角三角形ABC中,∠ACB=90,作CM平分∠ACB交AB于点M,点D为射线CM上一点,以点C为旋转中心将线段CD逆时针旋转90°得到线段CE,连接DE交射线CB于点F,连接BD、BE
填空:
①线段BD、BE的数量关系为______.
②线段BC、DE的位置关系为______.
推广:
(2)如图②,在等腰三角形ABC中,顶角∠ACB=a,作CM平分∠ACB交AB于点M,点D为△ABC外部射线CM上一点,以点C为旋转中心将线段CD逆时针旋转α度得到线段CE,连接DE、BD、BE请判断(1)中的结论是否成立,并说明理由.
应用:
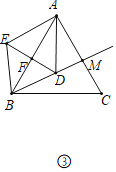
(3)如图③,在等边三角形ABC中,AB=4.作BM平分∠ABC交AC于点M,点D为射线BM上一点,以点B为旋转中心将线段BD逆时针旋转60°得到线段BE,连接DE交射线BA于点F,连接AD、AE.当以A、D、M为顶点的三角形与△AEF全等时,请直接写出DE的值.

【答案】(1)①BD=CE;②BD⊥CE;(2)结论:(1)中的结论仍然成立,理由见解析;(3)满足条件的DE的值为![]() 或4
或4![]() .
.
【解析】
①由CA=CB,∠ACB=90°,CM平分∠ACB,得出∠ECF=∠DCF=45°,易证△CBD≌△CBE,即可得出BD=BE;
②由CD=CE即可得出BC⊥DE.
(2)由CA=CB,∠ACB=α,CM平分∠ACB,得出∠ECF=∠DCF=![]() α,易证△CBD≌△CBF,即可得出BD=BE,再由等腰三角形的性质得出BC⊥DE.
α,易证△CBD≌△CBF,即可得出BD=BE,再由等腰三角形的性质得出BC⊥DE.
(3)分两种情况,根据三角形全等的性质及三角函数即可得出.
(1)如图①中,
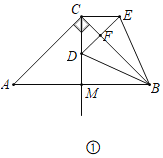
∵CA=CB,∠ACB=90°,CM平分∠ACB,
∴∠ACM=∠BCM=45°,
∵∠ECD=90°,
∴∠ECF=∠DCF=45°,
∵CD=CE,CB=CB,
∴△CBD≌△CBE(SAS),
∴BD=BE,
∵CD=CE,
∴BC垂直平分线段DE,
∴BC⊥DE.
故答案为BD=CE,BD⊥CE.
(2)结论:(1)中的结论仍然成立.
理由:如图②中,
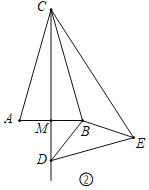
∵CA=CB,∠ACB=α,CM平分∠ACB,
∴∠ACM=∠BCM=![]() α,
α,
∵∠ECD=α,
∴∠ECF=∠DCF=![]() α,
α,
∵CD=CE,CB=CB,
∴△CBD≌△CBF(SAS),
∴BD=BE,
∵CD=CE,
∴BC垂直平分线段DE,
∴BC⊥DE.
(3)如图③中,
当△AFE≌△AMD时,AF=AM,
∵∠AFD=∠AMD=90°,
∵AD=AD,
∴Rt△ADF≌Rt△ADM(HL),
∴∠DAF=∠DAM=30°,
∴∠DBA=∠DAB=30°,
∴DA=DB,
∵DF⊥AB,
∴∠BDF=60°,BF=AF=2,
∵BD=BE,
∴△BDE是等边三角形,
∴DF=EF=BFtan30°=![]() ,
,
∴DE=2EF=![]() .
.
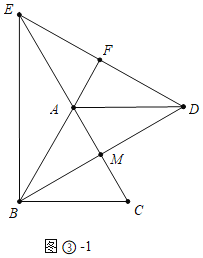
如图③-1中,当点D在AM的延长线时,易证AF=AM=2,DE=2DF=4![]() .
.
综上所述,满足条件的DE的值为![]() 或4
或4![]() .
.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案【题目】某超市销售进价为2元的雪糕,在销售中发现,此商品的日销售单价x(元)与日销售量y(根)之间有如下关系:
日销售单价x(元) | 3 | 4 | 5 | 6 |
日销售量y(根) | 40 | 30 | 24 | 20 |
(1)猜测并确定y和x之间的函数关系式;
(2)设此商品销售利润为W,求W与x的函数关系式,若物价局规定此商品最高限价为10元/根,你是否能求出商品日销售最大利润?若能请求出,不能请说明理由.