ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌOЮЊзјБъдЕуЃЌЕуAЕФзјБъЮЊЃЈЉ8ЃЌ0ЃЉЃЌжБЯпBCОЙ§ЕуBЃЈЉ8ЃЌ6ЃЉЃЌCЃЈ0ЃЌ6ЃЉЃЌНЋЫФБпаЮOABCШЦЕуOАДЫГЪБеыЗНЯђа§зЊНЧЖШІСЕУЕНЫФБпаЮOAЁфBЁфCЁфЃЌДЫЪББпOAЁфгыБпBCНЛгкЕуPЃЌБпBЁфCЁфгыBCЕФбгГЄЯпНЛгкЕуQЃЌСЌНгAPЃЎ
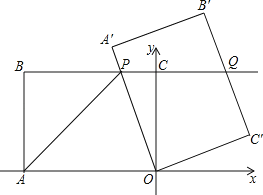
ЃЈ1ЃЉЫФБпаЮOABCЕФаЮзДЪЧ ЃЎ
ЃЈ2ЃЉдка§зЊЙ§ГЬжаЃЌЕБЁЯPAO=ЁЯPOAЃЌЧѓPЕузјБъЃЎ
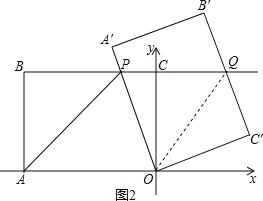
ЃЈ3ЃЉдка§зЊЙ§ГЬжаЃЌЕБPЮЊЯпЖЮBQжаЕуЪБЃЌСЌНгOQЃЌЧѓЁїOPQЕФУцЛ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉОиаЮЃЛЃЈ2ЃЉPЃЈЉ4ЃЌ6ЃЉЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉРћгУAЃЌBЃЌCЕузјБъЕУГіЁЯCOA=ЁЯOAB=ЁЯB=90ЁуЃЌНјЖјЕУГіД№АИЃЛ
ЃЈ2ЃЉРћгУЁЯPAO=ЁЯPOAЕУГіPA=POЃЌНјЖјЕУГіAE=EO=4ЃЌМДПЩЕУГіPЕузјБъЃЛ
ЃЈ3ЃЉЪзЯШЕУГіRtЁїOCQЁеRtЁїOC'QЃЈHLЃЉЃЌНјЖјРћгУЦНааЯпЕФаджЪЧѓГіЁЯPOQ=ЁЯPQOЃЌМДПЩЕУГіBP=POЃЌдйРћгУЙДЙЩЖЈРэЕУГіPQЕФГЄЃЌНјЖјЧѓГіЁїOPQЕФУцЛ§ЃЎ
НтЃКЃЈ1ЃЉЁпЕуAЕФзјБъЮЊЃЈЉ8ЃЌ0ЃЉЃЌЕуBЃЈЉ8ЃЌ6ЃЉЃЌCЃЈ0ЃЌ6ЃЉЃЌ
ЁрЁЯCOA=ЁЯOAB=ЁЯB=90ЁуЃЌ
ЁрЫФБпаЮOABCЪЧОиаЮЃЎ
ЙЪД№АИЮЊЃКОиаЮЃЛ
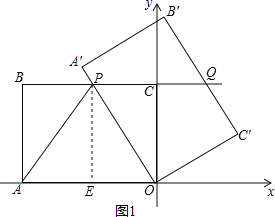
ЃЈ2ЃЉШчЭМ1ЃЌЙ§ЕуPзїPEЁЭAOгкЕуEЃЌ
ЁпЁЯPAO=ЁЯPOAЃЌ
ЁрPA=POЃЌ
ЁпPEЁЭAOЃЌ
ЁрAE=EO=4ЃЌ
ЁрPЃЈЉ4ЃЌ6ЃЉЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌдкRtЁїOCQКЭRtЁїOC'QжаЃЌ
![]() ЃЌ
ЃЌ
ЁрRtЁїOCQЁеRtЁїOC'QЃЈHLЃЉЃЌ
ЁрЁЯOQC=ЁЯOQC'ЃЌ
гжЁпOPЁЮC'QЃЌ
ЁпЁЯPOQ=ЁЯOQC'ЃЌ
ЁрЁЯPOQ=ЁЯPQOЃЌ
ЁрPO=PQЃЌ
ЁпBP=QPЃЌ
ЁрBP=OP=xЃЌ
дкRtЁїOPCжаЃЌx2=ЃЈ8ЉxЃЉ2+62ЃЌ
НтЕУЃКx=![]() ЃЎ
ЃЎ
ЙЪSЁїOPQ=![]() ЁСCOЁСPQ=
ЁСCOЁСPQ=![]() ЁС6ЁС
ЁС6ЁС![]() =
=![]() ЃЎ
ЃЎ