��Ŀ����
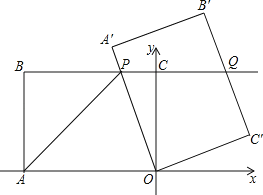
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A����Ϊ��2��4����ֱ��x=2��x���ཻ�ڵ�B������OA�����κ���y=x2ͼ��ӵ�O��OA����ƽ�ƣ���ֱ��x=2���ڵ�P������M��A��ʱֹͣ�ƶ���
��1�����߶�OA����ֱ�ߵĺ�������ʽ��
��2������κ�������M�ĺ�����Ϊm����mΪ��ֵʱ���߶�PB��̣���������κ����ı���ʽ��
��3�����߶�PB���ʱ�����κ�����ͼ���Ƿ����Q��a��a��1������˵���ɣ�
���𰸡���1��y=2x����2��y=��x��1��2+2����3�����κ�����ͼ����Q��
��������
�����������1�����ݴ���ϵ������ü��ɣ�
��2����������õ�����M��m��2m��������ƽ�Ƶ����ʺͶ�������õ������ߵĽ���ʽΪy=��x��m��2+2m����x=2�������ʽ���P�������꣬�������PB=m2��2m+4=��m��1��2+3��0��m��2�������ݶ��κ��������ʵó���m=1ʱ��PB��̣�������õ�PB���ʱ�������ߵĽ���ʽΪy=��x��1��2+2��
��3�������κ�����ͼ���ǹ���Q��a��a��1�����������ʽ�õ�����a��1=��a��1��2+2����������0���˷����⣬˵���˶��κ�����ͼ����Q��
�⣺��1����ֱ��OA�Ľ���ʽΪy=kx��
��A��2��4����
��2k=4�����k=2��
���߶�OA����ֱ�ߵĺ�������ʽΪy=2x��
��2��������M�ĺ�����Ϊm������OA���ƶ���
��y=2m��0��m��2����
��M��m��2m����
�������ߵĽ���ʽΪy=��x��m��2+2m��
����x=2ʱ��y=��2��m��2+2m=m2��2m+4��0��m��2����
��PB=m2��2m+4=��m��1��2+3��0��m��2����
����m=1ʱ��PB��̣�
��PB���ʱ�������ߵĽ���ʽΪy=��x��1��2+2��
��3�������κ�����ͼ���ǹ���Q��a��a��1��
��a��1=��a��1��2+2�н⣮
������a2��3a+4=0�н⣬
�ߡ�=����3��2��4��1��4=��7��0��
�����κ�����ͼ����Q��

 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д�