题目内容
【题目】如图所示,点A的坐标为A(0,a),将点A向右平移b个单位得到点B,其中a,b满足:(3a﹣2b)2+|a+b﹣5|=0. 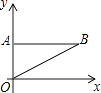
(1)求点B的坐标并求△AOB的面积S△AOB;
(2)在x轴上是否存在一点D,使得S△AOB=2S△AOD?若存在,求出D点的坐标;若不存在,说明理由.
【答案】
(1)解:∵(3a﹣2b)2+|a+b﹣5|=0,
∴ ![]() ,
,
解得: ![]() ,
,
∴B(3,2);
S△AOB= ![]() ×2×(3﹣0)=3
×2×(3﹣0)=3
(2)解:设D(x,0),
∵S△AOB=2S△AOD,
∴2× ![]() ×2|x|=3,
×2|x|=3,
解得:x=﹣ ![]() ,或
,或 ![]() ,
,
D为(﹣ ![]() ,0)或(
,0)或( ![]() ,0)
,0)
【解析】(1)根据非负数的性质求得a,b即可;(2)设D(x,0),根据S△AOB=2S△AOD即可求得x的长,进而求得D的坐标.
【考点精析】通过灵活运用三角形的面积和坐标与图形变化-平移,掌握三角形的面积=1/2×底×高;新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等即可以解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目