题目内容
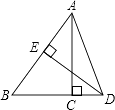
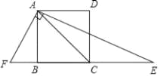
【题目】如图,正方形ABCD边长为1,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CE于点F,则EF的长为____.
【答案】2![]()
【解析】
利用正方形的性质和勾股定理可得AC的长,由角平分线的性质和平行线的性质可得∠CAE=∠E,易得CE=CA,由FA⊥AE,可得∠FAC=∠F,易得CF=AC,可得EF的长.
解:∵四边形ABCD为正方形,且边长为1,
∴AC=![]() ,
,
∵AE平分∠CAD,
∴∠CAE=∠DAE,
∵AD∥CE,
∴∠DAE=∠E,
∴∠CAE=∠E,
∴CE=CA=![]() ,
,
∵FA⊥AE,
∴∠FAC+∠CAE=90°,∠F+∠E=90°,
∴∠FAC=∠F,
∴CF=AC=![]() ,
,
∴EF=CF+CE=![]() +
+![]() =2
=2![]() .
.
故答案为:2![]() .
.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目