题目内容
【题目】已知AM∥BN，AE平分∠BAM，BE平分∠ABN，
（1）求∠AEB的度数．
（2）如图2，过点E的直线交射线线AM于点C，交射线BN于点D，求证：AC+BD＝AB；
（3）如图3，过点E的直线交射线线AM的反向延长线于点C，交射线BN于点D，AB＝5，AC＝3，S△ABE﹣S△ACE＝2，求△BDE的面积．
【答案】(1) ∠AEB=90°；（2）见解析；（3）8.
【解析】
（1）根据平行线的性质得到∠BAM+∠ABN=180°，根据角平分线的定义得到∠BAE=
∠BAM，∠ABE=∠ABN，于是得到结论；
（2）在AB上截取AF=AC，连接EF，证明△ACE≌△AFE，根据全等三角形的性质得到∠AEC=∠AEF，然后证明△BFE≌△BDE，得到BF=BD，等量代换即可得到结论；
（3）延长AE交BD于F，根据等腰三角形的性质得到AB=BF=5，AE=EF，根据全等三角形的性质得到DF=AC=3，设S△BEF=S△ABE=5x，S△DEF=S△ACE=3x，根据S△ABE-S△ACE=2，即可得到结论．
解：（1）∵AM∥BN，
∴∠BAM+∠ABN=180°，
∵AE平分∠BAM，BE平分∠ABN，
∴∠BAE=∠BAM，∠ABE=∠ABN，
∴∠BAE+∠ABE=（∠BAM+∠ABN）=90°，
∴∠AEB=90°；
（2）在AB上截取AF=AC，连接EF，
在△ACE与△AFE中，
，
∴△ACE≌△AFE，
∴∠AEC=∠AEF，
∴∠AEB=90°，
∴∠AEF+∠BEF=∠AEC+∠BED=90°，
∴∠FEB=∠DEB，
在△BFE与△BDE中，
，
∴△BFE≌△BDE，
∴BF=BD，
∵AB=AF+BF，
∴AC+BD=AB；
（3）延长AE交BD于F，
∵∠AEB=90°，
∴BE⊥AF，BE平分∠ABN，
∴AB=BF=5，AE=EF，
∵AM∥BN，
∴∠C=∠EDF，
在△ACE与△FDE中，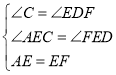
，
∴△ACE≌△FDE，
∴DF=AC=3，
∵BF=5，
∴设S△BEF=S△ABE=5x，S△DEF=S△ACE=3x，
∵S△ABE-S△ACE=2，
∴5x-3x=2，
∴x=1，
∴△BDE的面积=8．
