��Ŀ����
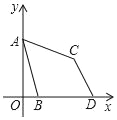
����Ŀ��(1)����������������Ľ���Ϊ���㣬�ֱ��������ƱȲ�Ϊ1�����������Σ�ʹ���ǣ��ٶ���ֱ�������Σ��ڶ�����������Σ��۶��Ƕ۽������Σ�
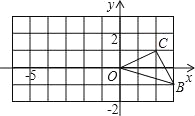
(2)��ͼ����֪O������ԭ�㣬B��C���������ֱ�Ϊ(3����1)��(2��1)��
����0��Ϊλ��������y�����ཫ��OBC�Ŵ�����(����ͼ��ԭͼ�����Ʊ�Ϊ2)������ͼ�Σ�
�ڷֱ�д��B��C����Ķ�Ӧ��B����C�������ꣻ
�������OBC�ڲ�һ��M������Ϊ(x��y)��д��M�Ķ�Ӧ��M�������꣮
���𰸡�(1)��������(2)�ټ���������B��(��6��2)��C��(��4����2)����M��(��2x����2y)��
��������
��1��������Ҫ��ͼ�μ��ɣ�
��2�������⻭��ͼ�Σ������ǽ���OBC�Ŵ�����������ǰ��������������λ��ͼ�Σ��ɹ���C��B�����ӳ�BO��CO��ʹ��OB��=2OB��OC��=2OC����ʹ�õ�����������ԭ����2�����ɣ���Ϊ�����ԭ��Գƣ���B��C���������֪�������ɵó����Ӧ������꣬���ڵ�M���������У��������Ӧ��Ҳ����ԭ��Գƣ���M�����꣬�����ɵ����Ӧ������꣮
�⣺(1)
�ٶ���ֱ��������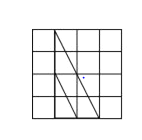
�ڶ������������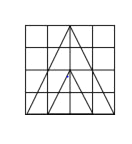
�۶��Ƕ۽�������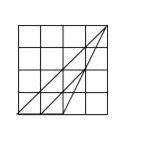 ��
��
(2) ����ͼ
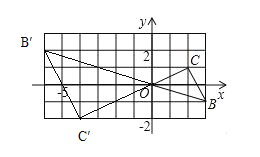
��B��������Ϊ(��6��2)��C��������Ϊ(��4����2)��
�ۡ�M������Ϊ(x��y)��
��M��������Ϊ(��2x����2y)��
�ʴ�Ϊ��(1)��������(2)�ټ���������B��(��6��2)��C��(��4����2)����M��(��2x����2y)��