Question

【题目】如下图，已知⊙O的直径为AB，AC⊥AB于点A, BC与⊙O相交于点D，在AC上取一点E，使得ED=EA．下面四个结论：①ED是⊙O的切线；②BC=2OE③△BOD为等边三角形；④△EOD ∽ △CAD，正确的是（ ）

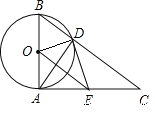
A. ①② B. ②④ C. ①②④ D. ①②③④

Answer 1

【答案】C

【解析】解：如图，连接OD．∵AC⊥AB，∴∠BAC=90°，即∠OAE=90°．在△AOE与△DOE中，∵OA=OD，AE=DE，OE=OE，∴△AOE≌△DOE（SSS），∴∠OAE=∠ODE=90°，即OD⊥ED．又∵OD是⊙O的半径，∴ED是⊙O的切线．故①正确；

∵△AOE≌△DOE，∴∠AOE=∠DOE，∵OB=OD，∴∠B=∠BDO，∵∠B+∠BDO=∠AOE+∠DOE，∴∠B=∠AOE，∴OE∥BC，∵AO=OB，∴OE是△BAC的中位线，∴BC=2OE,故②正确；

∵OE∥BC，∴∠AEO=∠C．∵△AOE≌△DOE，∴∠DEO=∠C，∠ODE=∠OAE=90°，∴∠ODE=ADC=90°，∴△EOD∽△CAD，∴正确的①②④．故选C．