Question

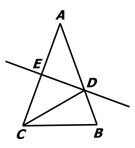
【题目】如图，正方形ABCD中，BE=EF=FC，CG=2GD，BG分别交AE，AF于M，N．下列结论：①AF⊥BG；②BN=NF；③；④．其中正确的结论的序号是______．

Answer 1

【答案】①③．

【解析】

①易证△ABF≌△BCG，即可解题；

②易证△BNF∽△BCG，即可求得的值，即可解题；

③作EH⊥AF，令AB=3，即可求得MN，BM的值，即可解题；

④连接AG，FG，根据③中结论即可求得S四边形CGNF和S四边形ANGD，即可解题．

①∵四边形ABCD为正方形，

∴AB=BC=CD，

∵BE=EF=FC，CG=2GD，

∴BF=CG，

∵在△ABF和△BCG中，

,

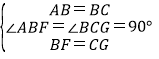∴△ABF≌△BCG，

∴∠BAF=∠CBG，

∵∠BAF+∠BFA=90°，

∴∠CBG+∠BFA=90°，即AF⊥BG；①正确；

②∵在△BNF和△BCG中，∠CBG=∠NBF，∠BCG=∠BNF=90°，

∴△BNF∽△BCG，

∴，

∴BN=NF；②错误；

③作EH⊥AF，令AB=3，则BF=2，BE=EF=CF=1，

AF==，

∵S△ABF=AFBN=ABBF，

∴BN=，NF=BN=，

∴AN=AF-NF=，

∵E是BF中点，

∴EH是△BFN的中位线，

∴EH=，NH=，BN∥EH，

∴AH=，

，解得：MN=，

∴BM=BN-MN=，MG=BG-BM=，

∴；③正确；

④连接AG，FG，根据③中结论，

则NG=BG-BN=，

∵S四边形CGNF=S△CFG+S△GNF=CGCF+NFNG=1+=，

S四边形ANGD=S△ANG+S△ADG=ANGN+ADDG=，

∴S四边形CGNF≠S四边形ANGD，④错误.

故选A．