题目内容
【题目】如图,在菱形ABCD中,点M、N在直线BD上,点M在N点左侧,AM∥CN.
(1)如图1,求证:BM=DN;
(2)如图2,当∠ABC=90°,点M,N在线段BD上时,求证:BM+BN= ![]() AB;
AB;
(3)如图3,当∠ABC=60°,点M在线段DB的延长线上时,直接写出BM,BN,AB三者的数量关系.
【答案】
(1)
解:∵四边形ABCD为菱形,
∴AB=CD,AB∥CD.
∴∠ABM=∠CDN.
∵AM∥CN,
∴∠AMN=∠MNC.
∴∠AMB=∠CND.
在△AMB和△CND中, 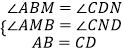
∴△AMB≌△CND.
∴MB=DN
(2)
解:由(1)得BM=DN.
∴BN+BM=DB.
当∠ABC=90°时,由勾股定理得;BD= ![]() =
= ![]() =
= ![]() AB.
AB.
∴MB+BN= ![]() AB
AB
(3)
解:NB﹣BM= ![]() AB.
AB.
如图1所示:过点A作AE⊥MN,垂足为E.
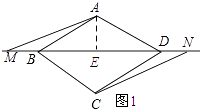
由(1)得BM=DN.
又∵BD=BN﹣DN,
∴BD=BN﹣BM.
当∠ABC=60°时,∠ABE=30°,
又∵∠AEB=90°,
∴AE= ![]() AB.
AB.
∴在Rt△ABE中,BE= ![]() =
= ![]() =
= ![]() AB.
AB.
∵AB=AD,AE⊥BD,
∴BE=ED.
∴BD= ![]() AB.
AB.
∴BN﹣BM= ![]() AB.
AB.
由勾股定理得;BD= ![]() =
= ![]() =
= ![]() AB.
AB.
∴MB+BN= ![]() AB
AB
【解析】(1)由菱形的性质可知AB=CD,AB∥CD,然后由平行线的性质和补角的性质∠ABM=∠CDN,∠AMB=∠CND,接下来依据AAS证明△AMB≌△CND,由全等三角形的性质可得到MB=DN;(2)由(1)得BM=DN,故此可得到BN+BM=DB,当∠ABC=90°时,在Rt△ABD中,由勾股定理可求得BD与AB的关系,从而得到BM+BN= ![]() AB;(3)过点A作AE⊥MN,垂足为E.由BM=DN可证明BD=BN﹣BM,当∠ABC=60°时,∠ABE=30°在Rt△ABE中,依据勾股定理可求得BE与AB的关系,然后再依据等腰三角形三线合一的性质可得到AB与BD的关系,于是得到BM,BN,AB三者的数量关系.
AB;(3)过点A作AE⊥MN,垂足为E.由BM=DN可证明BD=BN﹣BM,当∠ABC=60°时,∠ABE=30°在Rt△ABE中,依据勾股定理可求得BE与AB的关系,然后再依据等腰三角形三线合一的性质可得到AB与BD的关系,于是得到BM,BN,AB三者的数量关系.
【考点精析】本题主要考查了菱形的性质的相关知识点,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能正确解答此题.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案

