题目内容
【题目】已知正方形ABCD，点E，F分别在射线AB，射线BC上，AE=BF，DE与AF交于点O.
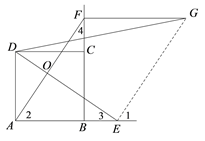
（1）如图1，当点E，F分别在线段AB，BC上时，则线段DE与AF的数量关系是 ，位置关系是 .
（2）如图2，当点E在线段AB延长线上时，将线段AE沿AF进行平移至FG，连接DG.
①依题意将图2补全；
②小亮通过观察、实验提出猜想：在点E运动的过程中，始终有
.
小亮把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：
想法1：连接EG，要证明
，只需证四边形FAEG是平行四边形及△DGE是等腰直角三角形.
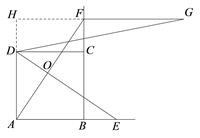
想法2：延长AD，GF交于点H，要证明
，只需证△DGH是直角三角形.
图1 图2
请你参考上面的想法，帮助小亮证明
.（一种方法即可）
【答案】（1）相等，垂直；（2）①补图见解析；②证明见解析
【解析】解：（1）相等，垂直．.
（2）①依题意补全图形．.
②法1：
证明：连接GE.
由平移可得AE=FG，AE∥FG，∴四边形AEGF是平行四边形.
∴AF=EG，AF∥EG，
∴∠1=∠2.
∵四边形ABCD是正方形，
∴AD = AB，∠DAE=∠ABC= 90°.
∵AE=BF，
∴△AED≌△BFA.
∴∠3=∠4，AF = DE.
∴EG=DE.
∵∠2+∠4=90°，
∴∠1+∠3=90°，∴∠DEG=90°.
∴
.
又 ∵
，
∴
.
法2：
证明：延长AD，GF交于点H，
由平移可得AE=FG，AE∥FG，
∴∠H+∠DAB= 180°
∵四边形ABCD是正方形，
∴∠DAB= 90°，AD=DC.
∴∠H = 90°.
∴
.
∵∠HDC=∠DCF= 90°,
∴四边形HDCF是矩形.
∴HF=DC.
∴HF=AD.
∵HG=FG+HF,
∴HG=AE+HF=AE+AD.
∵易证BF=AH 且BF=AE,
∴HD=AE –AD.
∴
.
