Question

【题目】已知D、E分别为△ABC中AB、BC上的动点，直线DE与直线AC相交于F，∠ADE的平分线与∠B的平分线相交于P，∠ACB的平分线与∠F的平分线相交于Q．

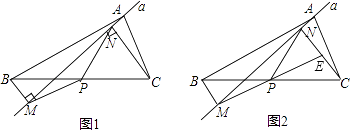
（1）如图1，当F在AC的延长线上时，求∠P与∠Q之间的数量关系；

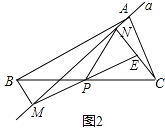
（2）如图2，当F在AC的反向延长线上时，求∠P与∠Q之间的数量关系（用等式表示）．

Answer 1

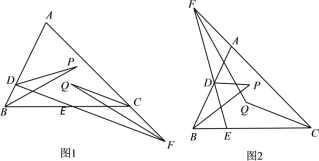
【答案】（1）∠P＝∠Q；（2）∠P＋∠Q＝180°．

【解析】

（1）先根据三角形内角和定理和三角形外角的性质求出2∠P=∠DEB，2∠Q=∠CEF，即可得出答案；

（2）先根据三角形内角和定理和三角形外角的性质求出∠P=∠BED，∠Q=90°+∠FEC，根据邻补角互补求出即可．

解：（1）∵DP是∠ADF的平分线，BP是∠ABC的平分线，

∴∠ADF=2∠ADP，∠ABC=2∠ABP，

∵∠ADF=∠ABC+∠DEB，∠ADP=∠P+∠ABP，

∴2∠ADP=2∠P+2∠ABP，

∴∠DEB=2∠P，

同理∠CEF=2∠Q，

∵∠DEB=∠CEF，

∴2∠P=2∠Q，

∴∠P=∠Q；

（2）∠P+∠Q=180°，

理由是：∵由（1）知：2∠P=∠BED，

∴∠P=∠BED，

∵FQ是∠CFE的平分线，CQ是∠ACB的平分线，

∴∠QFC=∠EFC，∠QCF=∠ACB，

∵∠FEC+∠EFC+∠ECF=180°，

∴∠EFC+∠ECF=180°-∠FEC，

∴∠Q=180°-（∠QFC+∠QCF）

=180°-（∠EFC+∠ECF）

=180°-（180°-∠FEC）

=90°+∠FEC，

∴∠P+∠Q=∠BED+90°+∠FEC

=90°+（∠BED+∠FEC）

=90°+×180°

=180°．