题目内容
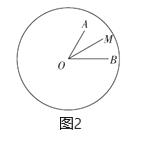
【题目】(本题满分10分)已知:如图,在△ABC中,D是AB边上一点,圆O过D、B、C三点,∠DOC=2∠ACD=90°.
(1)求证:直线AC是圆O的切线;
(2)如果∠ACB=75°,圆O的半径为2,求BD的长.

【答案】(1)见解析;(2)2
【解析】(1)证明:
∵2∠ACD=90°,
∴∠ACD=45°![]()
∵∠DOC=90°,且DO=CO,
∴△OCD为等腰直角三角形,∠OCD=45°![]()
∴∠ACO=∠ACD+∠DCO=45°+45°=90°
∴直线AC是⊙O的切线.![]()
(2)解:连接BO,
∵∠ACB=75°,∠ACD=45°,
∴∠DCB=30°,∴∠DOB=60°,![]()
∵DO=BO,
∴△BDO为等边三角形,![]()
∴BD=OB=4.![]()
(1)利用切线的判定定理求出∠ACO=∠ACD+∠DCO=45°+45°=90°,即可得出答案;
(2)利用圆周角定理得出△BDO为等边三角形,即可得出答案.

 53天天练系列答案
53天天练系列答案【题目】《中国诗词大会》是央视首档全民参与的诗词节目,节目以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨,其中的一个比赛环节“飞花令”增加了节目悬念.新学期开学,某班组织了甲、乙两组同学进行了“飞花令”的对抗赛,规定说对一首得1分,比赛中有一方说出9首就结束两个人对抗,得6分以上为合格,得9分以上为优秀,甲、乙两组同学的一次测试成绩如下:
甲组:9,4,6,5,9,6,7,6,8,6,9,5,7,6,9
乙组:4,6,7,6,7,9,7,5,8,7,6,7,9,6,8
(1)请你根据所给的两组数据,绘制统计图(表).
(2)把下面的表格补充完整.
统计量 | 平均分(分) | 方差(分2) | 中位数(分) | 合格率 | 优秀率 |
甲组 | 2.56 | 6 | 80.0% | 26.7% | |
乙组 | 6.8 | 1.76 | 86.7% | 13.3% |
(3)根据第(2)题表中数据,你会支持哪一组,并说明理由.