题目内容
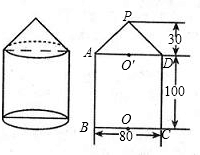
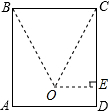
圆柱体内挖去一个与它不等高的圆锥,如其实物图和其剖面图所示.锥顶O到AD的距离为1,∠OCD=30°,OC=4,则挖去后该物体的表面积是______.
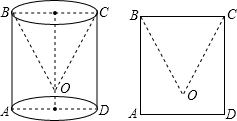

过点O作OE⊥CD于点E,
∵∠OCD=30°,OC=4,
∴sin30°=
=
,
解得:EO=2,
cos30°=
=
=
,
解得:EC=2
,
故由题意可得出:圆锥底面半径为2,DC=1+EC=1+2
,
则圆锥侧面积为:S=π×底面圆的半径×母线=π×2×4=8π,圆柱底面圆的面积为:π×2 2=4π,
圆柱侧面积为:底面圆的周长×圆柱的高=2×π×2×(1+2
)=4π+8
π,
故该物体的表面积=圆锥侧面积+圆柱底面圆的面积+圆柱侧面积=8π+4π+4π+8
π=(16+8
)π.
故答案为:(16+8
)π.
∵∠OCD=30°,OC=4,
∴sin30°=
| OE |
| OC |
| OE |
| 4 |
解得:EO=2,
cos30°=
| EC |
| CO |
| EC |
| 4 |
| ||
| 2 |
解得:EC=2
| 3 |
故由题意可得出:圆锥底面半径为2,DC=1+EC=1+2
| 3 |
则圆锥侧面积为:S=π×底面圆的半径×母线=π×2×4=8π,圆柱底面圆的面积为:π×2 2=4π,
圆柱侧面积为:底面圆的周长×圆柱的高=2×π×2×(1+2
| 3 |
| 3 |
故该物体的表面积=圆锥侧面积+圆柱底面圆的面积+圆柱侧面积=8π+4π+4π+8
| 3 |
| 3 |
故答案为:(16+8
| 3 |


练习册系列答案
相关题目