题目内容
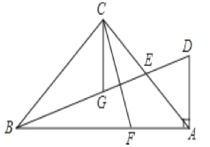
【题目】如图,![]() 中,
中,![]() ,连接
,连接![]() ,将
,将![]() 绕点
绕点![]() 旋转,当
旋转,当![]() (即
(即![]() )与
)与![]() 交于一点
交于一点![]() ,
,![]() (即
(即![]() )与
)与![]() 交于一点
交于一点![]() 时,给出以下结论:①
时,给出以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 的周长的最小值是
的周长的最小值是![]() .其中正确的是( )
.其中正确的是( )
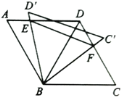
A. ①②③B. ①②④C. ②③④D. ①③④
【答案】B
【解析】
根据题意可证△ABE≌△BDF,可判断①②③,由△DEF的周长=DE+DF+EF=AD+EF=4+EF,则当EF最小时△DEF的周长最小,根据垂线段最短,可得BE⊥AD时,BE最小,即EF最小,即可求此时△BDE周长最小值.
解:∵AB=BC=CD=AD=4,∠A=∠C=60°
∴△ABD,△BCD为等边三角形,
∴∠A=∠BDC=60°,
∵将△BCD绕点B旋转到△BC'D'位置,
∴∠ABD'=∠DBC',且AB=BD,∠A=∠DBC',
∴△ABE≌△BFD,
∴AE=DF,BE=BF,∠AEB=∠BFD,
∴∠BED+∠BFD=180°,
故①正确,③错误;
∵∠ABD=60°,∠ABE=∠DBF,
∴∠EBF=60°,
故②正确
∵△DEF的周长=DE+DF+EF=AD+EF=4+EF,
∴当EF最小时,∵△DEF的周长最小.
∵∠EBF=60°,BE=BF,
∴△BEF是等边三角形,
∴EF=BE,
∴当BE⊥AD时,BE长度最小,即EF长度最小,
∵AB=4,∠A=60°,BE⊥AD,
∴EB=![]() ,
,
∴△DEF的周长最小值为4+![]() ,
,
故④正确,
综上所述:①②④说法正确,
故选:B.

练习册系列答案
相关题目