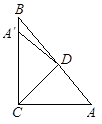题目内容
完成下列各题:
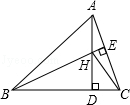
(1)如图,已知AC⊥BC,BD⊥AD,AC 与BD 交于O,AC=BD.求证:BC="AD."
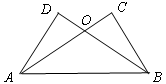
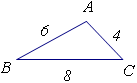
(2)如图,在△ABC中,∠A=30°,∠B=45°,AC= ,求AB的长.
,求AB的长.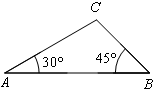
(1)如图,已知AC⊥BC,BD⊥AD,AC 与BD 交于O,AC=BD.求证:BC="AD."

(2)如图,在△ABC中,∠A=30°,∠B=45°,AC=
 ,求AB的长.
,求AB的长.
(1)由公共边AB= BA,AC=BD,根据“HL”证得△ACB≌△BDA,问题得证;(2)3+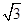
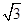
试题分析:(1)由公共边AB= BA,AC=BD,根据“HL”证得△ACB≌△BDA,问题得证;
(2)作CD⊥AB于点D,先根据含30°的直角三角形的性质求得CD、AD的长,再根据等腰直角三角形的性质求的BD的长,从而可以得到结果.
(1)∵AC⊥BC,BD⊥AD
∴∠D =∠C=90°
在Rt△ACB和 Rt△BDA 中,AB= BA,AC=BD,
∴△ACB≌ △BDA(HL)
∴BC=AD;
(2)作CD⊥AB于点D,

∵∠A=30°,AC=2
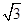 ,
,∴CD=
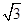
∴AD=3
又∵∠B=45°
∴BD=CD=
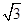
∴AB=AD+BD=3+
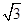
点评:解题的关键是熟练掌握含30°角的直角三角形的性质:30°角所对的直角边等于斜边的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目