题目内容
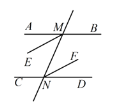
【题目】如图,已知直线AB∥CD,直线![]() 分别交
分别交![]() ,
,![]() 于
于![]() ,
,![]() 两点,若
两点,若![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的角平分线,试说明:ME∥NF.
的角平分线,试说明:ME∥NF.
解:∵AB∥CD,(已知)
∴![]() ,( )
,( )
∵![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的角平分线,(已知)
的角平分线,(已知)
∴∠EMN= ∠AMN,
∠FNM= ∠DNM,(角平分线的定义)
∴![]() ,(等量代换)
,(等量代换)
∴ME∥NF,( )
由此我们可以得出一个结论:两条平行线被第三条直线所截,一对 角的平分线互相 .
【答案】两直线平行内错角相等 ![]()
![]() 内错角相等两直线平行 内错 平行
内错角相等两直线平行 内错 平行
【解析】
先根据两直线平行内错角相等,可得∠AMN=∠DNM,然后根据角平分线的定义可得∠EMN=![]() ∠AMN,∠FNM=
∠AMN,∠FNM=![]() ∠DNM,然后根据等量代换可得∠EMN=∠FNM,然后根据内错角相等两直线平行即可说明ME∥NF.
∠DNM,然后根据等量代换可得∠EMN=∠FNM,然后根据内错角相等两直线平行即可说明ME∥NF.
解:∵AB∥CD,(已知)
∴∠AMN=∠DNM,(两直线平行内错角相等)
∵ME、NF分别是∠AMN、∠DNM的角平分线,(已知)
∴∠EMN=![]() ∠AMN,
∠AMN,
∠FNM=![]() ∠DNM,(角平分线的定义)
∠DNM,(角平分线的定义)
∴∠EMN=∠FNM(等量代换)
∴ME∥NF,(内错角相等两直线平行).
由此我们可以得出一个结论:两条平行线被第三条直线所截,一对内错角的平分线互相平行.
故答案为:两直线平行内错角相等 ![]()
![]() 内错角相等两直线平行 内错 平行
内错角相等两直线平行 内错 平行

【题目】在6.26国际禁毒日到来之际,某市教委为了普及禁毒知识,提高禁毒意识,举办了“关爱生命,拒绝毒品”的知识竞赛,某校七年级、八年级分别有300人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如下:
七年级 | 68 | 88 | 100 | 100 | 79 | 94 | 89 | 85 | 100 | 88 |
100 | 90 | 98 | 97 | 77 | 94 | 96 | 100 | 92 | 67 | |
八年级 | 69 | 97 | 91 | 69 | 98 | 100 | 99 | 100 | 90 | 100 |
99 | 89 | 97 | 100 | 99 | 94 | 79 | 99 | 98 | 79 |
(1)根据上述数据,将下列表格补充完成.
(整理、描述数据):
分数段 |
|
|
|
|
七年级人数 | 2 | ___________ | ___________ | 12 |
八年级人数 | 2 | 2 | 1 | 15 |
(分析数据):样本数据的平均数、中位数如下表:
年级 | 平均数 | 中位数 |
七年级 | 90.1 | 93 |
八年级 | 92.3 | ___________ |
(得出结论):
(2)你认为哪个年级掌握禁毒知识的总体水平较好,从两个方面说明你的理由.