Question

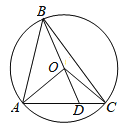
【题目】如图，已知四边形ABCD内接于圆，对角线AC与BD相交于点E，F在AC上，AB=AD,∠BFC=∠BAD=2∠DFC ．

(1)若∠DFC=40，求∠CBF的度数．

(2)求证: CD⊥DF ．

Answer 1

【答案】（1）50；（2）见解析

【解析】

（1）根据圆周角定理及三角形的外角，等腰三角形的知识进行角度的换算即可得；

（2）根据圆的内接四边形对角互补的性质进行角度计算即可证明．

解:(1)∵∠BAD=∠BFC，

∠BAD=∠BAC+∠CAD, ∠BFC=∠BAC+∠ABF,

∴∠CAD=∠ABF

又∵∠CAD=∠CBD,

∴∠ABF=∠CBD

∴∠ABD=∠FBC，

又

，

，

，

，

．

(2)令，则，

∵四边形是圆的内接四边形，

∴，即，

又∵，

∴，

∴

∴

∴，即．