题目内容
【题目】已知:抛物线![]()
![]() .
.
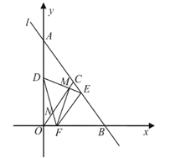
(1)求证:抛物线与![]() 轴有两个交点.
轴有两个交点.
(2)设抛物线与![]() 轴的两个交点的横坐标分别为
轴的两个交点的横坐标分别为![]() ,
,![]() (其中
(其中![]() ).若
).若![]() 是关于
是关于![]() 的函数、且
的函数、且![]() ,求这个函数的表达式;
,求这个函数的表达式;
(3)若![]() ,将抛物线向上平移一个单位后与
,将抛物线向上平移一个单位后与![]() 轴交于点
轴交于点![]() 、
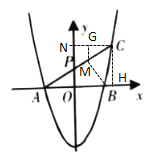
、![]() .平移后如图所示,过
.平移后如图所示,过![]() 作直线
作直线![]() ,分别交
,分别交![]() 的正半轴于点
的正半轴于点![]() 和抛物线于点
和抛物线于点![]() ,且
,且![]() .
.![]() 是线段
是线段![]() 上一动点,求
上一动点,求![]() 的最小值.
的最小值.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() 的最小值
的最小值![]()
【解析】
(1)通过计算判别式的值,即可得到结论;
(2)根据一元二次方程的求根公式,用含a的代数式表示抛物线与![]() 轴的两个交点的横坐标
轴的两个交点的横坐标![]() ,
,![]() ,即可得到答案;
,即可得到答案;
(3)易得直线![]() ,然后联立:
,然后联立: ,求出点C的坐标,过
,求出点C的坐标,过![]() 作
作![]() 轴于点N,过
轴于点N,过![]() 作
作![]() 于点
于点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,把
,把![]() 的最小值化为2(MB+GM)的最小值,即可得到答案.
的最小值化为2(MB+GM)的最小值,即可得到答案.
(1)∵![]() ,
,
![]() ,
,
![]() ,
,
∴抛物线与![]() 轴有两个交点;
轴有两个交点;
(2)令![]() ,则
,则![]() ,
,
![]() 或
或![]() ,
,
![]() ,
,
![]() 且
且![]() ,
,
![]() ,
,![]() ,
,
![]() ,即:
,即:![]() ;
;
(3)当![]() ,则
,则![]() ,向上平移一个单位得:
,向上平移一个单位得:![]() .
.
令![]() ,则
,则![]() 得:
得:![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 直线
直线![]() ,
,
联立: ,解得:
,解得: ,
,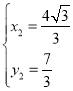 ,
,
即![]() ,
,
过![]() 作
作![]() 轴于点N,过
轴于点N,过![]() 作
作![]() 于点
于点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,
,
![]() 轴,
轴,
∴![]() ,
,
![]() ,
,
![]() ,
,
∵MB+GM≥CH,
![]() 的最小值=CH=
的最小值=CH=![]() ,
,
![]() 的最小值=
的最小值=![]() .
.

练习册系列答案
相关题目
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量![]() (袋
(袋![]() 与销售单价
与销售单价![]() (元
(元![]() 之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5.另外每天还需支付其他各项费用80元.
之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5.另外每天还需支付其他各项费用80元.
销售单价 | 3.5 | 5.5 |
销售量 | 280 | 120 |
(1)请求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)设每天的利润为![]() 元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?