Question

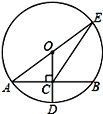
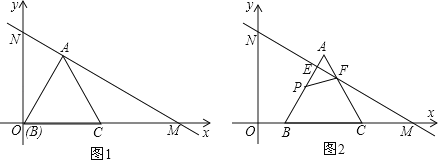
【题目】如图1，在平面直角坐标系xOy中，直线MN分别与x轴正半轴、y轴正半轴交于点M、N，且OM=6cm，∠OMN=30°，等边△ABC的顶点B与原点O重合，BC边落在x轴的正半轴上，点A恰好落在线段MN上，如图2，将等边△ABC从图1的位置沿x轴正方向以1cm/s的速度平移，边AB、AC分别与线段MN交于点E、F，在△ABC平移的同时，点P从△ABC的顶点B出发，以2cm/s的速度沿折线B→A→C运动，当点P达到点C时，点P停止运动，△ABC也随之停止平移．设△ABC平移时间为t（s），△PEF的面积为S（cm2）．

（1）求等边△ABC的边长；

（2）当点P在线段BA上运动时，求S与t的函数关系式，并写出自变量t的取值范围；

（3）点P沿折线B→A→C运动的过程中，是否在某一时刻，使△PEF为等腰三角形？若存在，求出此时t值；若不存在，请说明理由．

Answer 1

【答案】(1)OA=3cm；（2）s= ;(3) 存在，t值为或2

【解析】试题分析：（1）根据，∠OMN=30°和△ABC为等边三角形，求证△OAM为直角三角形，然后即可得出答案；（2）根据OM=6cm，∠OMN=30°，利用勾股定理求出MN和ON的长，再根据△OMN∽△BEM，利用其对应边成比例求出BE、PE，然后利用三角形面积公式即可求得答案；（3）△PEF为等腰三角形，求出t的值，如果在0＜t＜3这个范围内就存在，否则就不存在．

试题解析：

(1)∵直线MN分别与x轴正半轴、y轴正半轴交于点M、N,OM=6cm,∠OMN=30，

∴∠ONM=60，

∵△ABC为等边三角形

∴∠AOC=60°，∠NOA=30°

∴OA⊥MN，即△OAM为直角三角形，

∴OA=OM=×6=3cm.

(2)∵OM=6cm,∠OMN=30°，

∴ON=2,MN=4.

∵△OMN∽△BEM，

∴，

∴，

解得BE= ，

当点P在BE上时，

PE=BEPB= 2t= ，

∵∠A=60°,∠AFE=30°，

∴EF=AE= (3BE)= (3)=t，

∴△PEF的面积S=×EF×PE=×t× ，

即S= (0<t<)

当点P在AE上时,PE=PBBE=2t=，

∵∠A=60°,∠AFE=30°，

∴EF=AE= (3BE)= (3)=t，

∴△PEF的面积S=×EF×PE=×t×，

即S=

(3)存在，有4种情况：

①当点P在线段AB上时，

点P在AB上运动的时间为s，

∵△PEF为等腰三角形,∠PEF=90,

∴PE=EF，

∵∠A=60,∠AFE=30，

∴EF=AE= (3BE)= (3)=t，

∴=t或=t，

解得t= 或> (故舍去)，

②当点P在AF上时，

若PE=PF时，点P为EF的垂直平分线与AC的交点，

此时P为直角三角形PEF斜边AF的中点，

∴PF=AP=2t3，

∵点P从△ABC的顶点B出发，以2cm/s的速度沿折线B→A→C运动，

∴0<t<3，

在直角三角形中，cos30°=，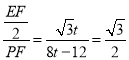

解得：t=2，

若FE=FP，

AF=EFcos∠AFE=EFcos30°=t，

则t(2t3)= t，

解得：t=126；

③当PE=EF，P在AE上时无解，

④当P点在CF上时,AP=2t3,AF=t,则PF=APAF=t3=EF,所以t3=t，

解得t=12+6>3，不合题意，舍去。

综上,存在t值为 或2时，△PEF为等腰三角形。