题目内容
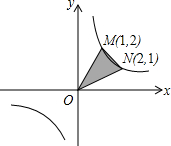
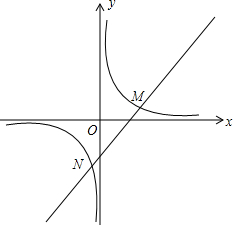
已知一次函数y=2x+n与反比例函数y=
的图象相交于M、N两点,且M为(2,1)
(1)求m、n的值及N的坐标.
(2)求△MON的面积.
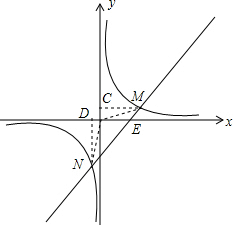
(3)如果过点M作MC⊥y轴于点C,过点N作ND⊥x轴于点D,试问直线CD与直线MN是否平行?证明你的猜想.
| m |
| x |
(1)求m、n的值及N的坐标.
(2)求△MON的面积.
(3)如果过点M作MC⊥y轴于点C,过点N作ND⊥x轴于点D,试问直线CD与直线MN是否平行?证明你的猜想.

(1)∵点M(2,1)在反比例函数y=
的图象上,
∴m=2×1=2,
∴反比例函数的解析式为:y=
;
∵点M(2,1)在一次函数y=2x+n的图象上,
∴4+n=1,解得n=-3,
∴一次函数y=2x+n的解析式为y=2x-3,
∴
,
解得
或
,
∴N(-
,-4);
(2)∵一次函数y=kx+b的解析式为y=2x-3,
∴E(
,0),
∵M(2,1),N(-
,-4),
∴S△MON=S△MOE+S△NOE=
×
×1+
×
×4=5;
(3)平行.
证明:∵M(2,1),N(-
,-4),
∴C(0,1),D(-
,0),
设直线CD的解析式为y=ax+b,则
,
解得
,
∴直线CD的解析式为;y=2x+1,
∵一次函数y=2x+n的解析式为y=2x-3,
∴直线CD与直线MN平行.
| m |
| x |
∴m=2×1=2,
∴反比例函数的解析式为:y=
| 2 |
| x |
∵点M(2,1)在一次函数y=2x+n的图象上,
∴4+n=1,解得n=-3,
∴一次函数y=2x+n的解析式为y=2x-3,
∴
|
解得
|
|
∴N(-
| 1 |
| 2 |
(2)∵一次函数y=kx+b的解析式为y=2x-3,
∴E(
| 3 |
| 2 |
∵M(2,1),N(-
| 1 |
| 2 |
∴S△MON=S△MOE+S△NOE=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
(3)平行.
证明:∵M(2,1),N(-
| 1 |
| 2 |
∴C(0,1),D(-
| 1 |
| 2 |
设直线CD的解析式为y=ax+b,则
|
解得
|
∴直线CD的解析式为;y=2x+1,
∵一次函数y=2x+n的解析式为y=2x-3,
∴直线CD与直线MN平行.


练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目