Question

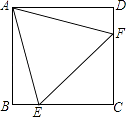
【题目】如图，在Rt△ABC中，∠ACB=90°，CD是边AB上的高．
（1）求证：△ABC∽△CBD；
（2）如果AC=4，BC=3，求BD的长．

Answer 1

【答案】
（1）证明：∵CD⊥AB，

∴∠BDC=90°．

∴∠A+∠ACD=90°．

∵∠ACB=90°，

∴∠DCB+∠ACD=90°．

∴∠A=∠DCB．

又∵∠ACB=∠BDC=90°，

∴△ABC∽△CBD；

（2）解：∵∠ACB=90°，AC=4，BC=3，

∴AB=5，

∴CD= ，

∵CD⊥AB，

∴BD= = = ．

【解析】（1）根据相似三角形的判定，由已知可证∠A=∠DCB，又因为∠ACB=∠BDC=90°，即证△ABC∽△CBD，（2）根据勾股定理得到AB=5，根据三角形的面积公式得到CD= ，然后根据勾股定理即可得到结论．