Question

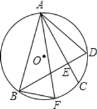
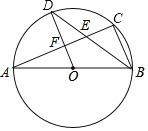
【题目】如图，AB是⊙O的直径，点C、D是⊙O上的点，且OD∥BC，AC分别与BD、OD相交于点E、F．

（1）求证：点D为的中点；

（2）若CB＝6，AB＝10，求DF的长；

（3）若⊙O的半径为5，∠DOA＝80°，点P是线段AB上任意一点，试求出PC+PD的最小值．

Answer 1

【答案】（1）见解析；（2）DF=2；（3）5

【解析】

（1）利用圆周角定理得到∠ACB＝90°，再证明OF⊥AC，然后根据垂径定理得到点D为的中点；

（2）证明OF为△ACB的中位线得到OF＝BC＝3，然后计算OD﹣OF即可；

（3）作C点关于AB的对称点C′，C′D交AB于P，连接OC，如图，利用两点之间线段最短得到此时PC+PD的值最小，再计算出∠DOC′＝120°，作OH⊥DC′于H，如图，然后根据等腰三角形的性质和含30度的直角三角形三边的关系求出DH，从而得到PC+PD的最小值．

（1）∵AB是⊙O的直径，

∴∠ACB＝90°，

∵OD∥BC，

∴∠OFA＝90°，

∴OF⊥AC，

∴＝，

即点D为的中点；

（2）解：∵OF⊥AC，

∴AF＝CF，

而OA＝OB，

∴OF为△ACB的中位线，

∴OF＝BC＝3，

∴DF＝OD﹣OF＝5﹣3＝2；

（3）解：作C点关于AB的对称点C′，C′D交AB于P，连接OC，如图，

∵PC＝PC′，

∴PD+PC＝PD+PC′＝DC′，

∴此时PC+PD的值最小，

∵＝，

∴∠COD＝∠AOD＝80°，

∴∠BOC＝20°，

∵点C和点C′关于AB对称，

∴∠C′OB＝20°，

∴∠DOC′＝120°，

作OH⊥DC′于H，如图，

则∠ODH＝30°，

则C′H＝DH，

在Rt△OHD中，OH＝OD＝，

∴DH＝OH＝，

∴DC′＝2DH＝5，

∴PC+PD的最小值为5．