题目内容
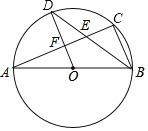
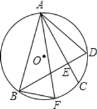
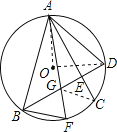
【题目】如图,半径为R的⊙O的弦AC=BD,AC、BD交于E,F为![]() 上一点,连AF、BF、AB、AD,下列结论:①AE=BE;②若AC⊥BD,则AD=
上一点,连AF、BF、AB、AD,下列结论:①AE=BE;②若AC⊥BD,则AD=![]() R;③在②的条件下,若
R;③在②的条件下,若![]() ,AB=
,AB=![]() ,则BF+CE=1.其中正确的是( )
,则BF+CE=1.其中正确的是( )
A.①②B.①③C.②③D.①②③
【答案】D
【解析】
①由弦AC=BD,可得![]() ,进而可得
,进而可得![]() ,然后由圆周角定理,证得∠ABD=∠BAC,即可判定AE=BE;②连接OA,OD,由AE=BE,AC⊥BD,可求得∠ABD=45°,进而可得△AOD是等腰直角三角形,则可求得AD=
,然后由圆周角定理,证得∠ABD=∠BAC,即可判定AE=BE;②连接OA,OD,由AE=BE,AC⊥BD,可求得∠ABD=45°,进而可得△AOD是等腰直角三角形,则可求得AD=![]() R;③设AF与BD相交于点G,连接CG,易证得△BGF是等腰三角形,CE=DE=EG,即可判断.
R;③设AF与BD相交于点G,连接CG,易证得△BGF是等腰三角形,CE=DE=EG,即可判断.
①∵弦AC=BD,
∴![]() ,
,
∴![]() ,
,
∴∠ABD=∠BAC,
∴AE=BE,故①正确;
②连接OA,OD,
∵AC⊥BD,AE=BE,
∴∠ABE=∠BAE=45,
∴∠AOD=2∠ABE=90,
∵OA=OD,
∴AD=![]() R,故②正确;
R,故②正确;
③设AF与BD相交于点G,连接CG,
∵![]() ,
,
∴∠FAC=∠DAC,
∵AC⊥BD,
∵在△AGE和△ADE中,
∵∠AEG=∠AED=90°,AE=AE,∠EAG=∠DAE,
∴△AGE≌△ADE(ASA),
∴AG=AD,EG=DE,
∴∠AGD=∠ADG,
∵∠BGF=∠AGD,∠F=∠ADG,
∴∠BGF=∠F,
∴BG=BF,
∵AC=BD,AE=BE,
∴DE=CE,
∴EG=CE,
∴BE=BG+EG=BF+CE,
∵AB=![]() ,
,
∴BE=ABcos45°=1,
∴BF+CE=1.
其中正确的是:①②③,故选D.

练习册系列答案
相关题目