题目内容
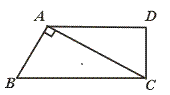
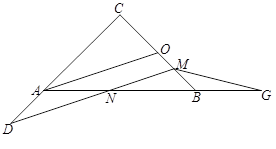
如图,已知 中,
中, ,
,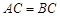 ,
,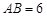 ,
, 是
是 边上的中点,
边上的中点, 是
是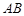 边上的点(不与端点重合),
边上的点(不与端点重合),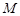 是
是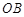 边上的点,且
边上的点,且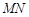 ∥
∥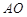 ,延长
,延长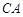 与直线
与直线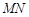 相交于点
相交于点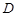 ,
,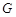 点是
点是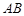 延长线上的点,且
延长线上的点,且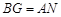 ,联结
,联结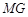 ,设
,设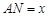 ,
,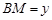 .
.
(1)求 关于
关于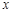 的函数关系式及其定义域;
的函数关系式及其定义域;
(2)联结 ,当以
,当以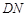 为半径的
为半径的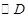 和以
和以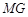 为半径的
为半径的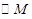 外切时,求
外切时,求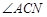 的正切值;
的正切值;
(3)当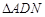 与
与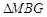 相似时,求
相似时,求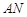 的长.
的长.
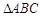 中,
中,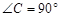 ,
,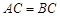 ,
,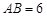 ,
, 是
是 边上的中点,
边上的中点, 是
是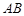 边上的点(不与端点重合),
边上的点(不与端点重合),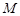 是
是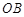 边上的点,且
边上的点,且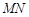 ∥
∥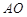 ,延长
,延长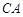 与直线
与直线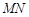 相交于点
相交于点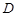 ,
,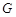 点是
点是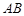 延长线上的点,且
延长线上的点,且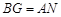 ,联结
,联结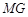 ,设
,设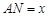 ,
,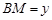 .
.
(1)求
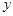 关于
关于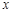 的函数关系式及其定义域;
的函数关系式及其定义域;(2)联结
 ,当以
,当以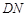 为半径的
为半径的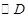 和以
和以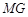 为半径的
为半径的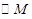 外切时,求
外切时,求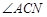 的正切值;
的正切值;(3)当
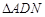 与
与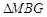 相似时,求
相似时,求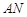 的长.
的长.(1)∵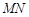 ∥
∥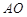 ,∴
,∴ ,
,
∵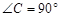 ,
,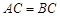 ,
,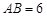 ,∴
,∴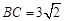 ,
,
∵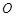 是
是 边上的中点,∴
边上的中点,∴ ,
,
∵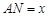 ,
,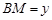 ,∴
,∴ ,∴
,∴ .
.
(2)∵以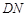 为半径的
为半径的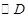 和以
和以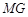 为半径的
为半径的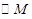 外切,
外切,
∴ ,又
,又 ,∴
,∴ ,
,
∴ , 又
, 又 ,∴
,∴ ,
,
∵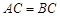 ,∴
,∴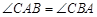 ,∴
,∴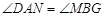 ,
,
又 ,∴
,∴ ≌
≌ , ∴
, ∴ ,
,
∵ ,∴
,∴ ,∴
,∴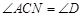 ,
,
∵ ,
,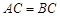 ,
,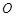 是
是 边上的中点,∴
边上的中点,∴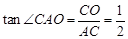 ,
,
∵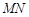 ∥
∥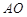 ,∴
,∴ ,∴
,∴ ,∴
,∴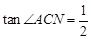 ,
,
(3)∵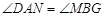 ,当
,当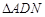 与
与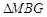 相似时,
相似时,
①若 时,过点
时,过点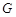 作
作 ,垂足为点
,垂足为点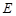 .
.
∴ ,∴
,∴ ,∴
,∴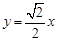 ,
,
又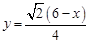 ,∴
,∴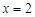 .
.
②若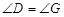 时,过点
时,过点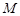 作
作 ,垂足为点
,垂足为点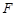 .
.
∴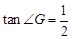 ,∴
,∴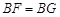 ,∴
,∴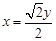 ,
,
又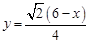 ,∴
,∴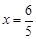 .
.
综上所述,当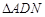 与
与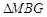 相似时,
相似时,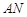 的长为2或
的长为2或 .
.
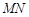 ∥
∥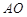 ,∴
,∴ ,
,∵
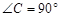 ,
,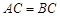 ,
,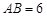 ,∴
,∴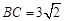 ,
,∵
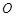 是
是 边上的中点,∴
边上的中点,∴ ,
, ∵
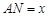 ,
,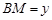 ,∴
,∴ ,∴
,∴ .
.(2)∵以
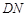 为半径的
为半径的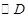 和以
和以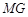 为半径的
为半径的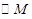 外切,
外切,∴
 ,又
,又 ,∴
,∴ ,
,∴
 , 又
, 又 ,∴
,∴ ,
,∵
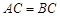 ,∴
,∴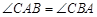 ,∴
,∴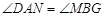 ,
,又
 ,∴
,∴ ≌
≌ , ∴
, ∴ ,
,∵
 ,∴
,∴ ,∴
,∴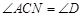 ,
, ∵
 ,
,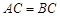 ,
,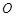 是
是 边上的中点,∴
边上的中点,∴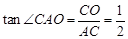 ,
, ∵
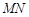 ∥
∥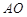 ,∴
,∴ ,∴
,∴ ,∴
,∴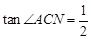 ,
,(3)∵
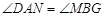 ,当
,当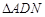 与
与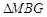 相似时,
相似时,①若
 时,过点
时,过点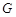 作
作 ,垂足为点
,垂足为点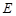 .
.∴
 ,∴
,∴ ,∴
,∴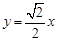 ,
, 又
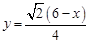 ,∴
,∴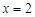 .
.②若
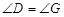 时,过点
时,过点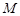 作
作 ,垂足为点
,垂足为点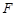 .
.∴
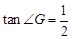 ,∴
,∴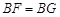 ,∴
,∴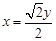 ,
, 又
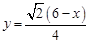 ,∴
,∴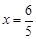 .
.综上所述,当
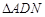 与
与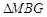 相似时,
相似时,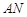 的长为2或
的长为2或 .
.本题主要考核一次函数解析式和定义域、三角函数和相似三角形的判定和性质

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
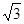 ,AE=3,求AF的长.
,AE=3,求AF的长.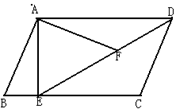

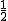 ,CE=2,则△ABC的周长是
,CE=2,则△ABC的周长是 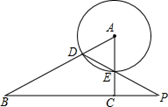
 BC,DE分别交边AB、AC于D、E两点,若△ADE与△ABC的面积比为1:9,则AD:AB的值为 .
BC,DE分别交边AB、AC于D、E两点,若△ADE与△ABC的面积比为1:9,则AD:AB的值为 .