题目内容
如图,在Rt△ABC中,∠ACB=90°,半径为1的圆A与边AB相交于点D,与边AC相交于点E,连接DE并延长,与线段BC的延长线交于点P.已知tan∠BPD=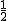 ,CE=2,则△ABC的周长是
,CE=2,则△ABC的周长是 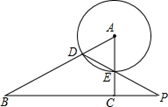
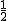 ,CE=2,则△ABC的周长是
,CE=2,则△ABC的周长是 
12
过D点作DQ⊥AC于点Q.
则△DQE与△PCE相似,设AQ=a,则QE=1-a.
∴ 且tan∠BPD=
且tan∠BPD=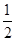 ,
,
∴DQ=2(1-a).
∵在Rt△ADQ中,据勾股定理得:AD2=AQ2+DQ2
即: ,
,
解之得a=1(不合题意,舍去),或a=.
∵△ADQ与△ABC相似,
∴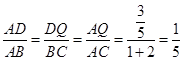 .
.
∴AB=5AD=5,BC=5DQ=4,AC=5AQ=3,
∴三角形ABC的周长是:AB+BC+AC=5+4+3=12;
故答案为:12.
则△DQE与△PCE相似,设AQ=a,则QE=1-a.
∴
 且tan∠BPD=
且tan∠BPD=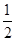 ,
,∴DQ=2(1-a).
∵在Rt△ADQ中,据勾股定理得:AD2=AQ2+DQ2
即:
 ,
,解之得a=1(不合题意,舍去),或a=.
∵△ADQ与△ABC相似,
∴
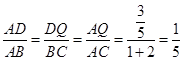 .
.∴AB=5AD=5,BC=5DQ=4,AC=5AQ=3,
∴三角形ABC的周长是:AB+BC+AC=5+4+3=12;
故答案为:12.

练习册系列答案
相关题目
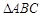 中,
中,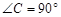 ,
,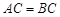 ,
, ,
,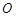 是
是 边上的中点,
边上的中点,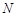 是
是 边上的点(不与端点重合),
边上的点(不与端点重合), 是
是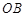 边上的点,且
边上的点,且 ∥
∥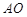 ,延长
,延长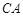 与直线
与直线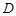 ,
, 点是
点是 ,联结
,联结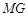 ,设
,设 ,
,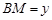 .
.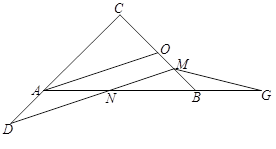
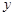 关于
关于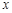 的函数关系式及其定义域;
的函数关系式及其定义域; ,当以
,当以 为半径的
为半径的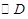 和以
和以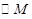 外切时,求
外切时,求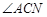 的正切值;
的正切值; 与
与 相似时,求
相似时,求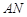 的长.
的长.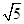 ;
;
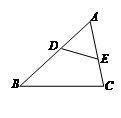
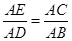

 = 。
= 。



