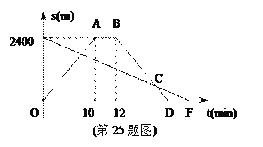
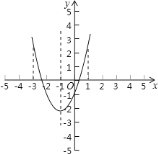
题目内容
【题目】已知四边形ABCD是正方形,△DEF是等腰直角三角形,DE=DF,M是EF的中点.

(1)如图1,当点E在AB上时,求证:点F在直线BC上.
(2)如图2,在(1)的条件下,当CM=CF时,求证:∠CFM=22.5°
(3)如图3,当点E在BC上时,若CM=2,则BE的长为 (直接写出结果)(注:等腰直角三角形三边之比为1:1:![]() )
)
【答案】(1)详见解析;(2)详见解析;(3)2![]()
【解析】
(1)根据四边形ABCD是正方形,△DEF是等腰直角三角形,利用SAS证明△ADE≌△CDF即可;
(2)作EN∥CM交BC于N,根据M是EF的中点得CM是△EFN的中位线,可证得△BEN是等腰直角三角形,利用外角的性质即可求证;
(3)过点F作FG⊥BC于G,FQ⊥AD于Q,过点E作EH⊥AD于H,则四边形CGQD为矩形,EH=AB=CD,作FN∥CM交CG于N,可根据AAS证明△QDF≌△HED,可得矩形CGQD是正方形,连接DM、GM,则DM是Rt△EDF的中线、GM是Rt△EGF的中线,可根据SSS证明△CMD≌△CMG,得到△NGF是等腰直角三角形,即可求出结果.
(1)证明:∵四边形ABCD是正方形,
∴AD=CD=AB=BC,∠A=∠BCD=∠ADC=90°,
∵△DEF是等腰直角三角形,
∴∠EDF=90°,
∴∠ADC=∠EDF,
∴∠ADE=∠CDF,
在△ADE和△CDF中, ,
,
∴△ADE≌△CDF(SAS),
∴∠A=∠DCF=90°,
∴点F在直线BC上;
(2)证明:作EN∥CM交BC于N,如图2所示:
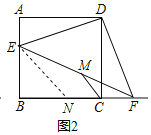
∵M是EF的中点,EN∥CM,
∴CM是△EFN的中位线,∠BCM=∠BNE,
∴CN=CF,由(1)得:△ADE≌△CDF,
∴AE=CF,
∴AE=CN,
∴BE=BN,
∴△BEN是等腰直角三角形,
∴∠BNE=45°,
∴∠BCM=45°,
∵CM=CF,
∴∠CMF=∠CFM=![]() ∠BCM=22.5°;
∠BCM=22.5°;
(3)解:过点F作FG⊥BC于G,FQ⊥AD于Q,则四边形CGQD为矩形,
过点E作EH⊥AD于H,则EH=AB=CD,
作FN∥CM交CG于N,如图3所示:
∵∠EDF=90°,
∴∠HDE+∠QDF=90°,
∵∠HDE+∠HED=90°,
∴∠QDF=∠HED,
在△QDF和△HED中,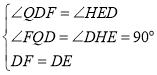 ,
,
∴△QDF≌△HED(AAS),
∴EH=DQ,
∴DQ=CD,
∴矩形CGQD是正方形,
∴CG=BC,
∵M是EF的中点,FN∥CM,
∴CM是△ENF的中位线,
∴∠GCM=∠GNF,NF=2CM=4,CE=CN,
∴BE=NG,
连接DM、GM,则DM是Rt△EDF的中线、GM是Rt△EGF的中线,
∴DM=![]() EF,GM=
EF,GM=![]() EF,
EF,
∴DM=GM,
在△CMD和△CMG中,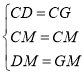 ,
,
∴△CMD≌△CMG(SSS),
∴∠DCM=∠GCM=![]() ∠DCG=45°,
∠DCG=45°,
∴∠GNF=45°,
∴△NGF是等腰直角三角形,
∴NG=![]() NF=
NF=![]() ,
,
故答案为:![]() .
.