题目内容
【题目】如图,在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
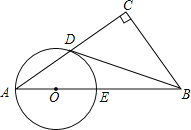
(1)求证:直线BD与⊙O相切;
(2)若AD:AE=![]() ,BC=6,求切线BD的长.
,BC=6,求切线BD的长.
【答案】(1)见解析;(2)3![]() .
.
【解析】
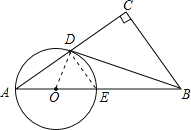
试题分析:(1)如图,连接OD,欲证明直线BD与⊙O相切,只需证明OD⊥BD即可;
(2)连接DE.利用圆周角定理和三角形中位线定理易求DE的长度,而AD:AE=![]() ,在直角△ADE中,利用勾股定理即可求得AE的长度;最后利用切割线定理来求切线BD的长度.
,在直角△ADE中,利用勾股定理即可求得AE的长度;最后利用切割线定理来求切线BD的长度.
(1)证明:∵OA=OD,
∴∠A=∠ADO(等边对等角).
又∵∠A+∠CDB=90°(已知),
∴∠ADO+∠CDB=90°(等量代换),
∴∠ODB=180°﹣(∠ADO+∠CDB)=90°,即BD⊥OD.
又∵OD是圆O的半径.
∴BD是⊙O切线;
(2)解:连接DE,则∠ADE=90°(圆周角定理).
∵∠C=90°,
∴∠ADE=∠C,
∴DE∥BC,
又∵D是AC中点,
∴DE是△ABC的中位线,
∴DE=![]() BC=3,AE=BE.
BC=3,AE=BE.
∵AD:AE=![]() ,
,
在直角△ADE中,利用勾股定理求得AE=3![]() ,则AB=6
,则AB=6![]() .
.
∴BD2=ABBE=6![]() ×3
×3![]() =54,
=54,
∴BD=3![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目