题目内容
如图，点E是BC的中点，∠BAE=∠CDE．求证：AB=CD．
证明：把CE绕C点顺时针旋转交DE于F，如图，
∴CE=CF，
∴∠1=∠2，
∴∠4=∠3，
∵点E是BC的中点，
∴BE=CE=CF，
在△BAE和△CDF中
，
∴△BAE≌△CDF（AAS），
∴AB=CD．
∴CE=CF，
∴∠1=∠2，
∴∠4=∠3，
∵点E是BC的中点，
∴BE=CE=CF，
在△BAE和△CDF中
|
∴△BAE≌△CDF（AAS），
∴AB=CD．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
导学与测试系列答案
相关题目
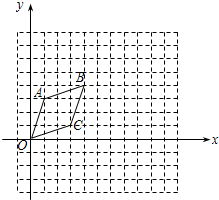
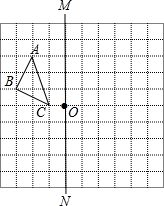
点上，在方格纸中建立平面直角坐标系如图所示．